
 =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ,以原點為圓點,橢圓的短半軸為半徑的圓與直線x-y+
,以原點為圓點,橢圓的短半軸為半徑的圓與直線x-y+ =0相切。
=0相切。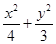 ="1." (Ⅱ)直線AE與x軸相交于定點Q(1,0)。
="1." (Ⅱ)直線AE與x軸相交于定點Q(1,0)。 =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 得到a,c的比值,以原點為圓點,橢圓的短半軸為半徑的圓與直線x-y+
得到a,c的比值,以原點為圓點,橢圓的短半軸為半徑的圓與直線x-y+ =0相切。那么利用線與圓相切,利用點到直線的距離公式得到圓的半徑。求解得到結論。
=0相切。那么利用線與圓相切,利用點到直線的距離公式得到圓的半徑。求解得到結論。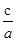 =
= ,所以e2=
,所以e2=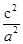 =
=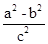 =
=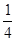 .即a2=
.即a2=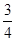 b2.
b2.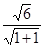 =
=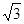 ,所以a2=4,b2=3.故橢圓的方程為
,所以a2=4,b2=3.故橢圓的方程為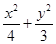 =1.…4分
=1.…4分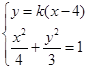 ,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分
,得(4k2+3)x2-32k2x+64k2-12=0. ①…6分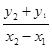 (x-x2).令y=0,得x=x2-
(x-x2).令y=0,得x=x2-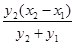 .將y1=k(x1-4),y2=k(x2-4)代入,
.將y1=k(x1-4),y2=k(x2-4)代入,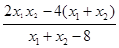 . ②…8分
. ②…8分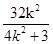 ,x1x2=
,x1x2=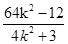 …10分 代入②整理,得x=1.
…10分 代入②整理,得x=1.

 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案科目:高中數學 來源:不詳 題型:填空題
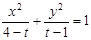 所表示的曲線為C,給出下列四個命題:
所表示的曲線為C,給出下列四個命題: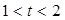 ,則C表是長軸在x軸上的橢圓.
,則C表是長軸在x軸上的橢圓.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
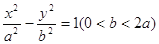 的左焦點
的左焦點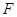 引圓
引圓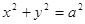 的切線,切點為T, 延長FT交雙曲線右支于點P, O為坐標原點,M為PF 的中點,則
的切線,切點為T, 延長FT交雙曲線右支于點P, O為坐標原點,M為PF 的中點,則 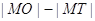 與
與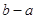 的大小關系為
的大小關系為 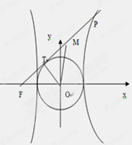
A.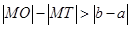 |
B.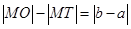 |
C.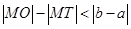 |
| D.不能確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com