
(滿分15分)設函數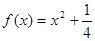 ,
,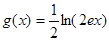 ,(其中
,(其中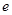 為自然底數);
為自然底數);
(Ⅰ)求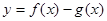 (
(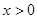 )的最小值;
)的最小值;
(Ⅱ)探究是否存在一次函數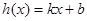 使得
使得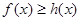 且
且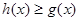 對一切
對一切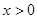 恒成立;若存在,求出一次函數的表達式,若不存在,說明理由;
恒成立;若存在,求出一次函數的表達式,若不存在,說明理由;
(Ⅲ)數列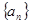 中,
中,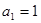 ,
,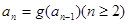 ,求證:
,求證: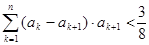 。
。
(Ⅰ)0(Ⅱ)存在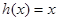 符合要求,理由見解析(Ⅲ)先證
符合要求,理由見解析(Ⅲ)先證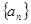 遞減且
遞減且 ,再利用放縮不等式證明
,再利用放縮不等式證明
【解析】
試題分析:(Ⅰ)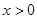 時
時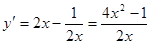 ,
,
易知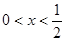 時
時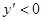 、
、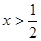 時
時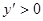 ;
;
所以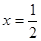 時求
時求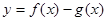 取最小值等于0; ……4分
取最小值等于0; ……4分
(Ⅱ)由題Ⅰ易知,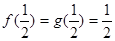 ,所以
,所以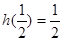 ; ……6分
; ……6分
所以可設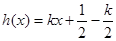 ,代入
,代入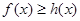
得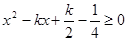 恒成立,所以
恒成立,所以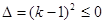 ,
,
所以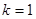 ,
,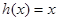 ; ……8分
; ……8分
此時設 ,
,
則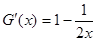 ,易知
,易知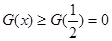 ,即
,即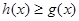 對一切
對一切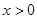 恒成立;
恒成立;
綜上,存在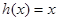 符合要求,它恰好是
符合要求,它恰好是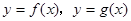 圖象的公切線. ……10分
圖象的公切線. ……10分
(Ⅲ)先證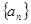 遞減且
遞減且 ;
;
由題(Ⅱ)知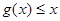 ,所以
,所以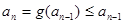 ,即
,即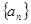 為遞減數列;
為遞減數列;
又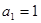 ,
,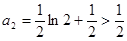 ,所以
,所以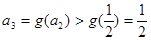 ,…
,…
因為當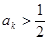 時總有
時總有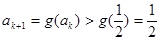 ,
,
所以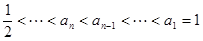 ; ……13分
; ……13分
所以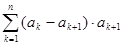
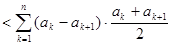
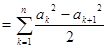
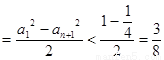 . ……15分
. ……15分
考點:本小題主要考查利用導數求最值、利用導數求解和恒成立問題和利用導數證明不等式,考查學生利用導數這個工具解決問題的能力和運算求解能力.
點評:導數是研究函數的性質如單調性、極值、最值等的有力工具,有時也用導數來解決實際應用題,要注意研究導數性質的時候不要忘記函數的定義域.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com