
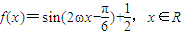 ,又
,又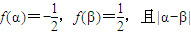 最小值為
最小值為 ,則正數ω的值為( )
,則正數ω的值為( )



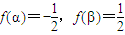 ,求得2ωα-
,求得2ωα-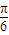 和2ωβ-
和2ωβ-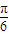 ,進而二者相減求得2ωα-2ωβ 的表達式,進而根據|α-β|的最小值為
,進而二者相減求得2ωα-2ωβ 的表達式,進而根據|α-β|的最小值為 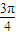 代入,根據ω為正整數,則可取k1=k2=1,求得答案.
代入,根據ω為正整數,則可取k1=k2=1,求得答案.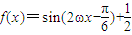 ,
,
 )=-1;
)=-1;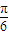 =(2k1+1)
=(2k1+1) ;
;
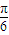 )=0;
)=0; =k2π;
=k2π; ;
;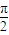 ;
; ,則
,則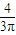 [(k1-k2)π+
[(k1-k2)π+ ]=
]= [4(k1-k2)+2]
[4(k1-k2)+2] [2(k1-k2)+1]
[2(k1-k2)+1]


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com