
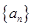 的前
的前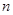 項和為
項和為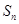 ,且滿足
,且滿足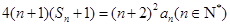 .
.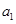 ,
,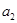 的值;
的值;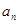 ;
;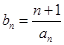 ,數列
,數列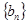 的前
的前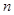 項和為
項和為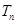 ,求證:
,求證: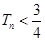 .
. (2)
(2) . (3)見解析
. (3)見解析 的定義即可求的
的定義即可求的 .
. 與
與 的關系(
的關系( ),即可消去
),即可消去 得到關于
得到關于 的遞推式,整理可后利用疊乘法即可得到
的遞推式,整理可后利用疊乘法即可得到 的通項公式,注意驗證首項.此外還可以先找規律得到通項公式,再利用數學歸納法進行證明.這也是可以的.
的通項公式,注意驗證首項.此外還可以先找規律得到通項公式,再利用數學歸納法進行證明.這也是可以的. 是不可求和的數列,可以考慮放縮成為可求和的數列,跟據
是不可求和的數列,可以考慮放縮成為可求和的數列,跟據 為分式,以此可以考慮放縮成為可以裂項求和的數列
為分式,以此可以考慮放縮成為可以裂項求和的數列 ,裂項求和即可證明相應的不等式.
,裂項求和即可證明相應的不等式. 時,有
時,有 ,解得
,解得 .
. 時,有
時,有 ,解得
,解得 . 2分
. 2分 時,有
時,有 , ①
, ① . ②
. ② ,即:
,即: . 5分
. 5分
 .
.

 . 8分
. 8分 .
. 當
當 時,有
時,有 ,
, 
 . 9分[
. 9分[ ,
, ,猜想:
,猜想: . 3分
. 3分 時,有
時,有 ,猜想成立.
,猜想成立. 時,猜想也成立,即:
時,猜想也成立,即: .
.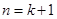 時,有
時,有 ,
, ,①
,① , ②
, ② ,
, .
. 當
當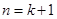 時,猜想也成立.
時,猜想也成立. 成立. 8分
成立. 8分
 , 10分
, 10分

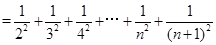


 . 14分
. 14分

科目:高中數學 來源:不詳 題型:單選題
 )(n∈N*)均在函數y=
)(n∈N*)均在函數y= x+
x+ 的圖象上,則a2014=( )
的圖象上,則a2014=( )| A.2014 | B.2013 | C.1012 | D.1011 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com