
��֪�E�A
 �ϵ��c(di��n)����ɽ��c(di��n)���x֮�͞�
�ϵ��c(di��n)����ɽ��c(di��n)���x֮�͞� �����^�c(di��n)
�����^�c(di��n) ��
��
������E�A���̣�
����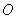 ������(bi��o)ԭ�c(di��n)��б�ʞ�
������(bi��o)ԭ�c(di��n)��б�ʞ� ��ֱ���^�E�A���ҽ��c(di��n)�����c�E�A�����c(di��n)
��ֱ���^�E�A���ҽ��c(di��n)�����c�E�A�����c(di��n)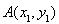 ��
��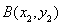 ����
����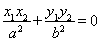 �����
�����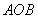 ����e.
����e.
���� ����1
����1
��������
ԇ�}�����������əE�A�Ķ��x���E�A�Ď����|(zh��)�� ��
��  �����ɵ���E�A���̡������O(sh��)��ֱ������
�����ɵ���E�A���̡������O(sh��)��ֱ������ ��Ȼ��(li��n)��������y����x���õ��P(gu��n)��x��һԪ���η��̣��ٸ���(j��)�f�_(d��)�����ó����cϵ��(sh��)���P(gu��n)ϵʽ�������
��Ȼ��(li��n)��������y����x���õ��P(gu��n)��x��һԪ���η��̣��ٸ���(j��)�f�_(d��)�����ó����cϵ��(sh��)���P(gu��n)ϵʽ������� �ٌ�
�ٌ�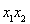 ��
�� ����
���� ���
��� ��ֵ�������L��ʽ���
��ֵ�������L��ʽ��� �������c(di��n)�����ľ��x��ʽ���c(di��n)
�������c(di��n)�����ľ��x��ʽ���c(di��n) ��ֱ��
��ֱ��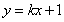 �ľ��x���˾��x�����
�ľ��x���˾��x����� ��߅
��߅ �ϵĸߡ�����������e��ʽ����á�
�ϵĸߡ�����������e��ʽ����á� ����e��
����e��
ԇ�}�������⣨�����}���� ��
�� ��
��
�ʙE�A���̞� �� ����
�� ����
������?y��n)�ֱ�� �^�ҽ��c(di��n)
�^�ҽ��c(di��n)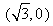 ���O(sh��)ֱ��
���O(sh��)ֱ��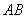 �ķ��̞�
�ķ��̞�  .
.
(li��n)�����̽M
��ȥ ��������
�������� �� ��*��
�� ��*��
�� ��
�� ��
��
 ��
��
�� ����
���� ��
��
���� ���ɵ�
���ɵ� ����
����  ��
��
���̣�*���ɻ��� ����
���� ���ɵ�
���ɵ� ��
��
ԭ�c(di��n) ��ֱ��
��ֱ�� �ľ��x
�ľ��x .
.
���� �� 13��
�� 13��
���c(di��n)��1�E�A�Ļ��A(ch��)֪�R��2ֱ���c�E�A��λ���P(gu��n)ϵ��3���L��ʽ��4�c(di��n)��ֱ���ľ��x��


 ���ŕ��I(y��)���㕽ӌ���������ϵ�д�
���ŕ��I(y��)���㕽ӌ���������ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
��֪�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() �����Ҝ�(zh��n)����
�����Ҝ�(zh��n)����![]() �ϴ����c(di��n)
�ϴ����c(di��n)![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �S�Ϸ�����ʹ
�S�Ϸ�����ʹ![]() ����������Σ�
�����������
�����x����![]() �ķ�����
�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2010��߿���(sh��)�W(xu��)С�}�ޕrӖ(x��n)��ԇ����07���������棩 �}�ͣ�����}
 �����ҽ��c(di��n)�քe��F1��F(xi��n)2�����Ҝ�(zh��n)����l�ϴ����c(di��n)A���c(di��n)A��x�S�Ϸ�����ʹ��AF1F2����������Σ�
�����ҽ��c(di��n)�քe��F1��F(xi��n)2�����Ҝ�(zh��n)����l�ϴ����c(di��n)A���c(di��n)A��x�S�Ϸ�����ʹ��AF1F2����������Σ� ���ɽ��c(di��n)F1��F(xi��n)2�ľ��x֮�͞�
���ɽ��c(di��n)F1��F(xi��n)2�ľ��x֮�͞� �����AF1F2�ă�(n��i)�ЈA�ķ��̣�
�����AF1F2�ă�(n��i)�ЈA�ķ��̣��鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com