
《萊因德紙草書》(Rhind Papyrus)是世界上最古老的數學著作之一。書中有一道這樣的題目:把100個面包分給五人,使每人成等差數列,且使最大的三份之和的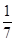 是較小的兩份之和,則最小1份的大小是
是較小的兩份之和,則最小1份的大小是

解析試題分析:設五個人所分得的面包為a-2d,a-d,a,a+d,a+2d,(其中d>0);
則,(a-2d)+(a-d)+a+(a+d)+(a+2d)=5a=100,∴a=20;
由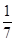 (a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=
(a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=
所以,最小的1分為a-2d=20-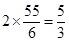 ,故答案為
,故答案為 。
。
考點:本題主要考查了等差數列模型的實際應用,解題時應巧設數列的中間項,從而容易得出結果
點評:解決該試題的關鍵是設五個人所分得的面包為a-2d,a-d,a,a+d,a+2d,(d>0);則由五個人的面包和為100,得a的值;由較大的三份之和的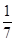 是較小的兩份之和,得d的值;從而得最小的1分a-2d的值.
是較小的兩份之和,得d的值;從而得最小的1分a-2d的值.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
傳說古希臘畢達哥拉斯學派的數學家經常在沙灘上畫點或用小石子表示數. 他們研究過如圖所示的三角形數: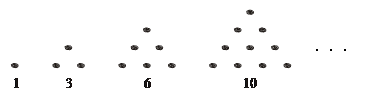
|
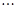 記為數列
記為數列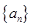 ,將可被5整除的三角形數按從小到大的順序組成一個新數列
,將可被5整除的三角形數按從小到大的順序組成一個新數列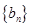 . 可以推測:(Ⅰ)
. 可以推測:(Ⅰ)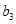 是數列
是數列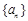 中的第 項;
中的第 項;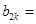 ________(用k表示)
________(用k表示)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列 的各項都是正數,且對任意
的各項都是正數,且對任意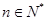 都有
都有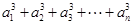
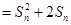 ,其中
,其中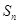 為數列
為數列 的前
的前 項和.
項和.
(1)求 、
、 ;
;
(2)求數列 的通項公式;
的通項公式;
(3)設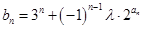 ,對任意的
,對任意的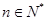 ,都有
,都有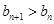 恒成立,求實數
恒成立,求實數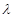 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
設數列 的前n項和為
的前n項和為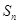 ,令
,令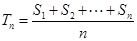 ,稱
,稱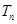 為數列
為數列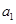 ,
,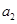 ,…,
,…, 的“理想數”,已知數列
的“理想數”,已知數列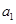 ,
,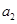 ,……,
,……,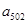 的“理想數”為2012,那么數列2,
的“理想數”為2012,那么數列2,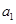 ,
,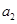 ,…,
,…,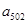 的“理想數”為( )
的“理想數”為( )
| A.2010 | B.2011 | C.2012 | D.2013 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com