
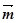 =(sinA,cosA),
=(sinA,cosA), 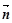 =
=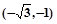 ,
,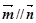 ,且A為銳角.
,且A為銳角.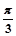 ;(2) f(x)有最大值
;(2) f(x)有最大值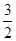 ,x=2kp+
,x=2kp+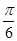 或x=2kp+
或x=2kp+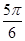 (kÎZ)
(kÎZ) 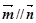 ∴-sinA+
∴-sinA+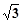 cosA=0 3分
cosA=0 3分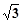 ,A為銳角,∴A=
,A為銳角,∴A=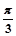 6分
6分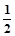
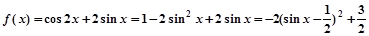 8分
8分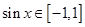 ,因此,當
,因此,當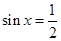 時,f(x)有最大值
時,f(x)有最大值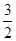 10分
10分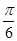 或x=2kp+
或x=2kp+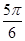 (kÎZ) 12分
(kÎZ) 12分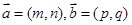 平行,等價于
平行,等價于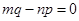 。利用向量的運算,得到三角函數(shù)式,運用三角公式進行化簡,以便于利用其它知識解題,是這類題的顯著特點。
。利用向量的運算,得到三角函數(shù)式,運用三角公式進行化簡,以便于利用其它知識解題,是這類題的顯著特點。

科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
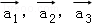 ;以C為起點,其余頂點為終點的向量分別為
;以C為起點,其余頂點為終點的向量分別為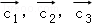 ,若i,j,k,l∈{1,2,3},且i≠j,k≠l,則
,若i,j,k,l∈{1,2,3},且i≠j,k≠l,則 的最小值是 .
的最小值是 .查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com