
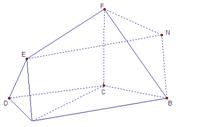
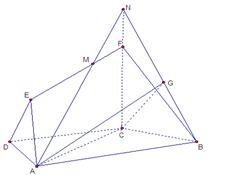
((本小題12分)如圖,在梯形 中,
中,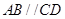 ,
, ,四邊形
,四邊形 為矩形,平面
為矩形,平面 平面
平面 ,
, .
.
(1)求證: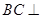 平面
平面 ;
;
(2)求二面角A-BF-C的平面角的余弦值;
(3)若點 在線段
在線段 上運動,設(shè)平面
上運動,設(shè)平面 與平面
與平面 所成二面角的平面角為
所成二面角的平面角為 ,試求
,試求 的取值范圍.
的取值范圍.

(1)證明:在梯形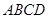 中,
∵
中,
∵ 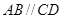 ,
,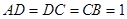 ,
,
∠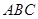 =
=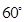 ,∴
,∴
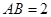 ∴
∴ 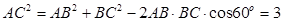
∴ 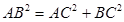 ∴
∴  ⊥
⊥
∵平面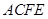 ⊥平面
⊥平面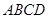 ,
,
平面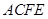 ∩平面
∩平面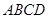
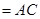 ,
,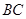
 平面
平面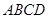
∴ 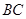 ⊥平面
⊥平面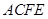
(2)取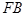 中點為
中點為 ,連結(jié)
,連結(jié)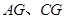
∵ 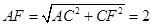 ,∴
,∴
 ∴
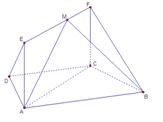
∴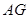 ⊥
⊥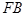 ∵
∵  ∴
∴  ⊥
⊥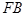 ∴ ∠
∴ ∠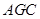 =
=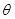
∵ 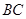 ⊥
⊥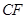 ∴
∴ 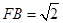 ∴
∴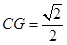 ,
,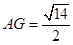
∴ 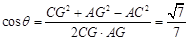
(3)由(2)知,①當(dāng)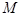 與
與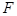 重合時,
重合時,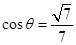
②當(dāng)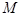 與
與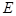 重合時,過
重合時,過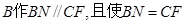 ,連結(jié)
,連結(jié) ,則平面
,則平面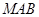 ∩平面
∩平面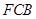 =
= ,∵
,∵ 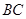 ⊥
⊥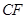 ,又∵
,又∵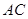 ⊥
⊥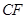 ∴
∴ 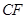 ⊥平面
⊥平面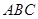 ∴
∴  ⊥平面
⊥平面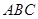
∴ ∠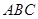 =
=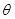 ∴
∴ 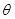 =
=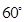 ,∴
,∴ 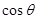 =
=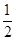
③當(dāng)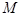 與
與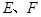 都不重合時,令
都不重合時,令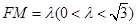
延長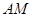 交
交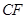 的延長線于
的延長線于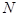 ,連結(jié)
,連結(jié)
∴ 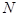 在平面
在平面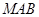 與平面
與平面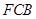 的交線上
的交線上
∵ 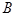 在平面
在平面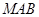 與平面
與平面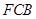 的交線上
的交線上
∴ 平面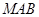 ∩平面
∩平面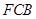 =
=
過C作CH⊥NB交NB于H ,連結(jié)AH,
由(I)知,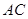 ⊥
⊥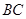 , 又∵AC⊥CN,∴ AC⊥平面NCB
, 又∵AC⊥CN,∴ AC⊥平面NCB
∴ AC⊥NB, 又∵ CH⊥NB,AC∩CH=C,∴ NB⊥平面ACH
∴AH⊥NB ∴ ∠AHC=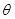
在 中,可求得NC=
中,可求得NC=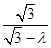 ,從而,在
,從而,在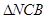 中,可求得CH=
中,可求得CH=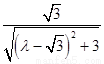
∵ ∠ACH=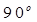 ∴ AH=
∴ AH=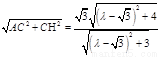
∴ 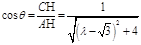 ∵
∵ 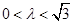 ∴
∴ 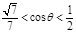 ,
綜上得
,
綜上得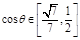 。
。
【解析】略


 全優(yōu)測試卷系列答案
全優(yōu)測試卷系列答案 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數(shù)學(xué) 來源:瀏陽一中、田中高三年級2009年下期期末聯(lián)考試題 數(shù)學(xué)試題 題型:解答題
(本小題12分)
如圖,曲線 是以原點
是以原點 為中心,以
為中心,以 、
、 為焦點的橢圓的一部分,曲線
為焦點的橢圓的一部分,曲線 是以
是以 為頂點,以
為頂點,以 為焦點的拋物線的一部分,
為焦點的拋物線的一部分, 是曲線
是曲線 和
和 的交點,且
的交點,且 為鈍角,若
為鈍角,若 ,
, .
.
(I)求曲線 和
和 所在的橢圓和拋物線的方程;
所在的橢圓和拋物線的方程;
(II)過 作一條與軸不垂直的直線,分別與曲線
作一條與軸不垂直的直線,分別與曲線 、
、 依次交于
依次交于 、
、 、
、 、
、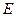 四點(如圖),若
四點(如圖),若 為
為 的中點,
的中點, 為
為 的中點,問
的中點,問 是否為定值?若是,求出定值;若不是,請說明理由.
是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011年新疆農(nóng)七七師高級中學(xué)高二下學(xué)期第一學(xué)段考試?yán)砜茢?shù)學(xué) 題型:解答題
(本小題12分)
如圖, <
< <
< <…<
<…< )是曲線C
)是曲線C
 :
: 上的n個點,點
上的n個點,點 在x軸的正半軸上,且⊿
在x軸的正半軸上,且⊿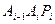 是正三角形(
是正三角形( 是坐標(biāo)原點)。
是坐標(biāo)原點)。
(1)寫出
(2)求出點 的橫坐標(biāo)
的橫坐標(biāo) 關(guān)于n的表達式并用數(shù)學(xué)歸納法證明
關(guān)于n的表達式并用數(shù)學(xué)歸納法證明
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年江西省協(xié)作體高三第三次聯(lián)考文科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題12分)如圖,直三棱柱 中,
中,
 ,
, 為
為 中點,若規(guī)定主視方向為垂直于平面
中點,若規(guī)定主視方向為垂直于平面 的方向,則可求得三棱柱左視圖的面積為
的方向,則可求得三棱柱左視圖的面積為 ;
;

(Ⅰ)求證: ;
;
(Ⅱ)求三棱錐 的體積。
的體積。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年四川省高2013屆春期重點班第一學(xué)月考試數(shù)學(xué)試題 題型:解答題
(本小題12分)如圖,B、A是某海面上位于東西方向相距 海里的兩個觀測點。現(xiàn)位于B點正北方向、A點北偏東
海里的兩個觀測點。現(xiàn)位于B點正北方向、A點北偏東 方向的C點有一艘輪船發(fā)出求救信號,位于B點北偏西
方向的C點有一艘輪船發(fā)出求救信號,位于B點北偏西 、A點北偏西
、A點北偏西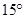 的D點的救援船立即前往營救,其航行速度為
的D點的救援船立即前往營救,其航行速度為 海里/小時.問該救援船到達C點需要多少時間?
海里/小時.問該救援船到達C點需要多少時間?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012年福建省四地六校高二第二次月考文科數(shù)學(xué) 題型:解答題
(本小題12分)
如圖4:求 的算法的
的算法的
程序框圖。⑴標(biāo)號①處填 。標(biāo)號②處填 。⑵根據(jù)框圖用直到型(UNTIL)語句編寫程序。

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com