
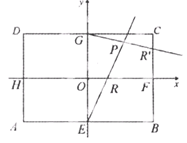
在矩形ABCD中,|AB|=2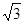 ,|AD|=2,E、F、G、H分別為矩形四條邊的中點,以HF、GE所在直線分別為x,y軸建立直角坐標系(如圖所示).若R、R′分別在線段0F、CF上,且
,|AD|=2,E、F、G、H分別為矩形四條邊的中點,以HF、GE所在直線分別為x,y軸建立直角坐標系(如圖所示).若R、R′分別在線段0F、CF上,且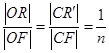 .
.
(Ⅰ)求證:直線ER與GR′的交點P在橢圓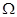 :
: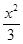 +
+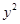 =1上;
=1上;
(Ⅱ)若M、N為橢圓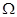 上的兩點,且直線GM與直線GN的斜率之積為
上的兩點,且直線GM與直線GN的斜率之積為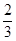 ,求證:直線MN過定點;并求△GMN面積的最大值.
,求證:直線MN過定點;并求△GMN面積的最大值.
 詳見解析;
詳見解析; 直線MN過定點(0,-3),△GMN面積的最大值
直線MN過定點(0,-3),△GMN面積的最大值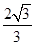 .
.
解析試題分析: 先計算出E、R、G、R′各點坐標,得出直線ER與GR′的方程,解得其交點坐標
先計算出E、R、G、R′各點坐標,得出直線ER與GR′的方程,解得其交點坐標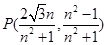 代入滿足橢圓方程即可;
代入滿足橢圓方程即可;  先討論直線MN的斜率不存在時的情況;再討論斜率存在時,用斜截式設出直線MN方程.與橢圓方程聯立,用“設而不求”的方法通過韋達定理得出b為定值-3或1,又當b=1時,直線GM與直線GN的斜率之積為0,所以舍去.從而證明出MN過定點(0,-3).最后算出點
先討論直線MN的斜率不存在時的情況;再討論斜率存在時,用斜截式設出直線MN方程.與橢圓方程聯立,用“設而不求”的方法通過韋達定理得出b為定值-3或1,又當b=1時,直線GM與直線GN的斜率之積為0,所以舍去.從而證明出MN過定點(0,-3).最后算出點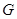 到直線
到直線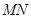 的距離及MN的距離,得出△GMN面積是一個關于
的距離及MN的距離,得出△GMN面積是一個關于 的代數式,由
的代數式,由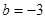 及
及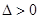 知:
知: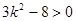 ,用換元法利用基本不等式求出△GMN面積的最大值是
,用換元法利用基本不等式求出△GMN面積的最大值是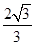 .
.
試題解析:(Ⅰ)∵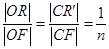 ,∴
,∴ ,
,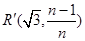 1分
1分
又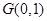 則直線
則直線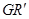 的方程為
的方程為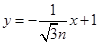 ① 2分
① 2分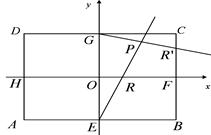
又 則直線
則直線 的方程為
的方程為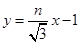 ②
②
由①②得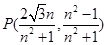
∵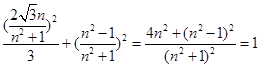
∴直線 與
與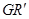 的交點
的交點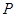 在橢圓
在橢圓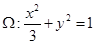 上 4分
上 4分
(Ⅱ)①當直線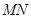 的斜率不存在時,設
的斜率不存在時,設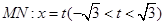
不妨取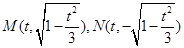 ∴
∴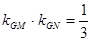 ,不合題意 5分
,不合題意 5分
②當直線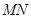 的斜率存在時,設
的斜率存在時,設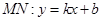
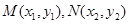

聯立方程 得
得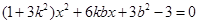
則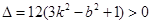
 7分
7分
又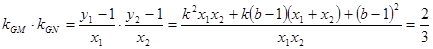
即
將 代入上式得
代入上式得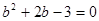
解得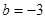 或
或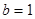 (舍)
(舍)
∴直線過定點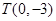 10分
10分
∴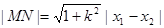 ,點
,點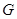 到直線
到直線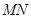 的距離為
的距離為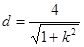
∴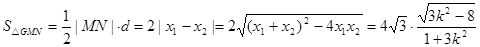
由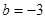 及
及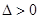 知:
知: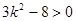 ,令
,令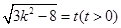 即
即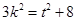
∴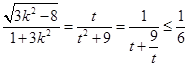 當且僅當
當且僅當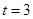 時,
時,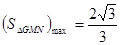 13分
13分
考點:1.直線的方程;2.解析幾何;3.基本不等式.


 備戰中考寒假系列答案
備戰中考寒假系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com