如圖,設有雙曲線

,F
1,F
2是其兩個焦點,點M在雙曲線上.
(1)若∠F
1MF
2=90°,求△F
1MF
2的面積;
(2)若∠F
1MF
2=60°,△F
1MF
2的面積是多少?若∠F
1MF
2=120°,△F
1MF
2的面積又是多少?
(3)觀察以上計算結(jié)果,你能看出隨∠F
1MF
2的變化,△F
1MF
2的面積將怎樣變化嗎?試證明你的結(jié)論.

(1)
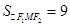
; (2)
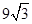
,
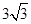
; (3) θ增大時面積變小,證明過程見解析.
試題分析:(1) 設
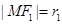
,
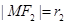
, 直角三角形△F
1MF
2中
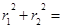
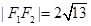
,利用雙曲線定義得
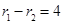
,平方得
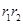
,求得面積;(2) △F
1MF
2 中由余弦定理可得,|MF
1|·|MF
2|,由面積公式
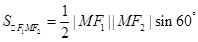
可得面積;(3) 由雙曲線定義與余弦定理,可得面積與θ的關系
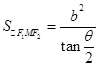
,所以θ增大時面積變小.
解:(1)由雙曲線方程知a=2,b=3,
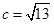
,
設
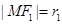
,
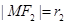
(
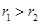
).
由雙曲線定義,有
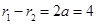
,兩邊平方得,
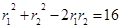
,
即
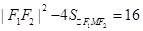
,
也即
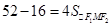
,求得
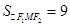
. 4分
(2)若∠F
1MF
2=60°,在△MF
1F
2中,
由余弦定理得
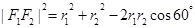
,
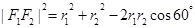
,所以
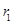
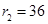
.
求得
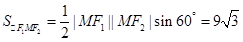
.
同理可求得若∠F
1MF
2=120°,
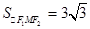
. 8分
(3)由以上結(jié)果猜想,隨著∠F
1MF
2的增大,△F
1MF
2的面積將減小.
證明如下:
令∠F
1MF
2=θ,則
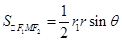
.
由雙曲線定義及余弦定理,有
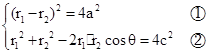
②-①得
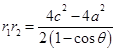
,
所以
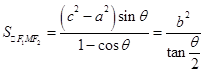
,
因為0<θ<π,
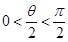
,
在
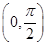
內(nèi),
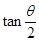
是增函數(shù),
因此當θ增大時,
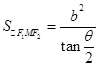
將減小. 12分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線

的左,右焦點分別為

,點P在雙曲線的右支上,且

,則此雙曲線的離心率e的最大值為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設圓C與兩圓(x+
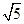
)
2+y
2=4,(x-
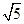
)
2+y
2=4中的一個內(nèi)切,另一個外切.
(1)求C的圓心軌跡L的方程;
(2)已知點M(
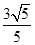
,
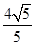
),F(xiàn)(
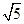
,0),且P為L上動點,求||MP|-|FP||的最大值及此時點P的坐標.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設直線
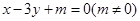
與雙曲線
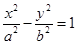
(
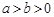
)兩條漸近線分別交于點
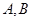
,若點
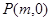
滿足
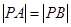
,則該雙曲線的離心率是__________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
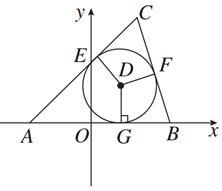
[2014·北京模擬]△ABC的頂點A(-5,0),B(5,0),△ABC的內(nèi)切圓圓心在直線x=3上,則頂點C的軌跡方程是________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知雙曲線
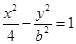
的右焦點與拋物線
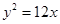
的焦點重合,則該雙曲線的焦點到其漸近線的距離等于( ).
A.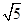 | B.4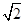 | C.3 | D.5 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設雙曲線
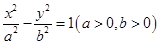
的離心率為
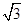
,且直線
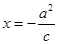
(c是雙曲線的半焦距)與拋物線
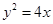
的準線重合,則此雙曲線的方程為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
雙曲線
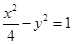
的離心率等于____________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知A
1,A
2雙曲線
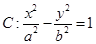
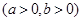
的頂點,B為雙曲線C的虛軸一個端點.若△A
1BA
2是等邊三角形,則雙曲線
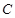
的離心率e等于
.
查看答案和解析>>

 ,F1,F2是其兩個焦點,點M在雙曲線上.
,F1,F2是其兩個焦點,點M在雙曲線上.
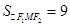 ; (2)
; (2) 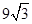 ,
,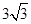 ; (3) θ增大時面積變小,證明過程見解析.
; (3) θ增大時面積變小,證明過程見解析.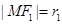 ,
,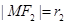 , 直角三角形△F1MF2中
, 直角三角形△F1MF2中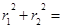
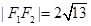 ,利用雙曲線定義得
,利用雙曲線定義得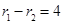 ,平方得
,平方得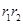 ,求得面積;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面積公式
,求得面積;(2) △F1MF2 中由余弦定理可得,|MF1|·|MF2|,由面積公式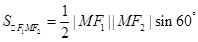 可得面積;(3) 由雙曲線定義與余弦定理,可得面積與θ的關系
可得面積;(3) 由雙曲線定義與余弦定理,可得面積與θ的關系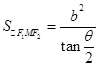 ,所以θ增大時面積變小.
,所以θ增大時面積變小.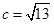 ,
,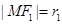 ,
,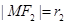 (
(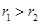 ).
).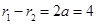 ,兩邊平方得,
,兩邊平方得,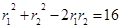 ,
,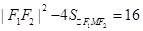 ,
,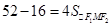 ,求得
,求得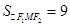 . 4分
. 4分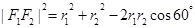 ,
,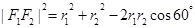 ,所以
,所以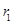
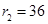 .
.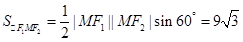 .
.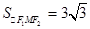 . 8分
. 8分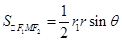 .
.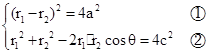
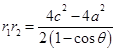 ,
,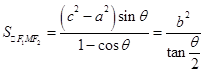 ,
,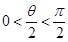 ,
,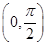 內(nèi),
內(nèi),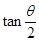 是增函數(shù),
是增函數(shù),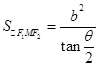 將減小. 12分
將減小. 12分

 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案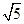 )2+y2=4,(x-
)2+y2=4,(x-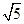 )2+y2=4中的一個內(nèi)切,另一個外切.
)2+y2=4中的一個內(nèi)切,另一個外切.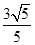 ,
,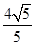 ),F(xiàn)(
),F(xiàn)(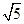 ,0),且P為L上動點,求||MP|-|FP||的最大值及此時點P的坐標.
,0),且P為L上動點,求||MP|-|FP||的最大值及此時點P的坐標.