
本小題滿分12分)設函數f(x)= 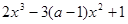 ,其中
,其中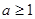
(1)求f(x)的單調區(qū)間;(2)討論f(x)的極值
(Ⅰ)當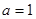 時,
時,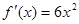 ,
,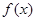 在
在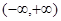 上單調遞增;
上單調遞增;
當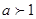 時,
時,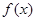 在
在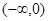 上單調遞增;在
上單調遞增;在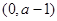 上單調遞減;在
上單調遞減;在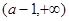 上單調遞增;
上單調遞增;
(Ⅱ)當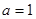 時,函數
時,函數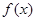 沒有極值;
沒有極值;
當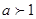 時,函數
時,函數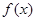 在
在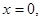 處取得極大值,在
處取得極大值,在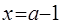 處取得極小值
處取得極小值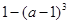 .
.
【解析】
試題分析: (1)先求解函數的導數,然后根據導數的正負解集,需要對參數a分類討論得到單調區(qū)間。
(2)在第一問的基礎上,利用函數的單調性確定極值問題。
解:由已知得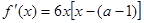 ,令
,令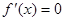 ,解得
,解得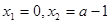 。。。。。。。2分
。。。。。。。2分
(Ⅰ)當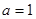 時,
時,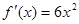 ,
,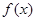 在
在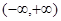 上單調遞增;。。。。。。。。。。。4分
上單調遞增;。。。。。。。。。。。4分
當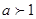 時,
時,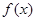 在
在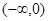 上單調遞增;在
上單調遞增;在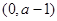 上單調遞減;在
上單調遞減;在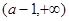 上單調遞增;.。。。6
上單調遞增;.。。。6
(Ⅱ)由(Ⅰ)知,當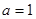 時,函數
時,函數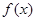 沒有極值;.。。。。。。。。。。。。。。。。。9分
沒有極值;.。。。。。。。。。。。。。。。。。9分
當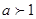 時,函數
時,函數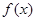 在
在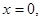 處取得極大值,在
處取得極大值,在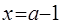 處取得極小值
處取得極小值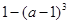 .。。。。。。。。12分
.。。。。。。。。12分
考點:本題主要考查了導數在研究函數中的運用。
點評:解決該試題的關鍵是利用導數來判定函數的單調性以及函數的極值問題,也是高考中常見的重要的題型,要給予關注。


科目:高中數學 來源: 題型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中數學 來源:2011屆吉林省油田中學高三第一次模擬考試數學理卷 題型:解答題
(本小題滿分12分)
設a∈R,函數f(x)= e -x(ax2 + a + 1),其中e是自然對數的底數;
(1)求函數f(x)的單調區(qū)間;
(2)當 -1<a<0 時,求函數f(x)在 [ 1,2 ] 上的最小值。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三教學質量檢測(四)文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)設平面向量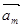 =(m,1),
=(m,1), 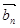 =(2,n),其中m,n∈{1,2,3,4}.
=(2,n),其中m,n∈{1,2,3,4}.
(Ⅰ)請列出有序數組(m,n)的所有可能結果;
(Ⅱ)若“使得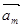 ⊥(
⊥(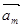 -
-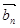 )成立的(m,n)”為事件A,求事件A發(fā)生的概率。
)成立的(m,n)”為事件A,求事件A發(fā)生的概率。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省萊蕪市高三上學期期末檢測理科數學 題型:解答題
(本小題滿分12分)
設 的內角A、B、C所對的邊分別為a、b、c,且
的內角A、B、C所對的邊分別為a、b、c,且 .
.
(1)當 時,求a的值;
時,求a的值;
(2)當 的面積為3時,求a+c的值。
的面積為3時,求a+c的值。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com