
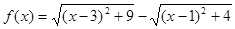 ,則
,則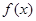 的最大值是 .
的最大值是 .科目:高中數(shù)學 來源:不詳 題型:解答題
 滿足
滿足 (
(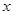 +2)=
+2)= (2-
(2-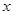 ),且方程
),且方程 的兩實根的平方和為10,
的兩實根的平方和為10, 的圖象過點(0,3),
的圖象過點(0,3), (
(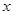 )的解析式.
)的解析式. 在
在 上的值域。
上的值域。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
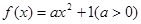 ,
,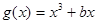
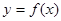 與曲線
與曲線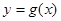 在它們的交點(1,c)處具有公共切線,求
在它們的交點(1,c)處具有公共切線,求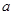 ,
,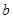 的值;
的值;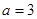 ,
,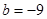 時,若函數(shù)
時,若函數(shù)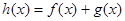 在區(qū)間[
在區(qū)間[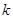 ,2]上的最大值為28,求
,2]上的最大值為28,求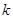 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
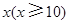 層,則每平方米的平均建筑費用為
層,則每平方米的平均建筑費用為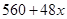 (單位:元).為了使樓房每平方米的平均綜合費用最少,該樓房應建為多少層?
(單位:元).為了使樓房每平方米的平均綜合費用最少,該樓房應建為多少層?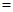 平均建筑費用
平均建筑費用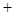 平均購地費用,平均購地費用
平均購地費用,平均購地費用 )
)查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
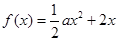 ,
,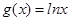 .
.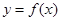 在
在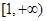 上是單調減函數(shù),求
上是單調減函數(shù),求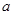 的取值范圍;
的取值范圍;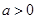 ,使得方程
,使得方程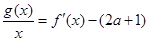 在區(qū)間
在區(qū)間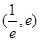 內有且只有兩個不相等的實數(shù)根?若存在,請求出
內有且只有兩個不相等的實數(shù)根?若存在,請求出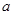 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少?方盒的最大容積為多少?
的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少?方盒的最大容積為多少?查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com