
設直線 是曲線
是曲線
 的一條切線,
的一條切線, .
.
(1)求切點坐標及 的值;
的值;
(2)當 時,存在
時,存在
 ,求實數
,求實數 的取值范圍.
的取值范圍.
(1)切點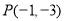 ,
,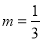 或者切點
或者切點 ,
, ;(2)
;(2) .
.
【解析】
試題分析:(1)先設切點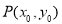 ,然后依題意計算出
,然后依題意計算出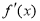 ,由
,由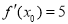 ,計算出切點的橫坐標,代入切線的方程,可得切點的縱坐標,最后再將切點的坐標代入曲線C的方程計算得
,計算出切點的橫坐標,代入切線的方程,可得切點的縱坐標,最后再將切點的坐標代入曲線C的方程計算得 的值;(2)結合(1)中求出的
的值;(2)結合(1)中求出的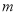 ,確定
,確定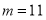 ,設
,設 ,然后將存在
,然后將存在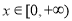 使
使 成立問題,轉化為
成立問題,轉化為 ,進而求出
,進而求出 ,分
,分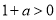 、
、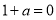 、
、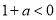 三種情況討論函數
三種情況討論函數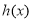 在
在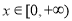 上的單調性,確定
上的單調性,確定 ,相應求解不等式
,相應求解不等式 ,即可確定
,即可確定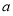 的取值范圍.
的取值范圍.
試題解析:(1)設直線 與曲線
與曲線 相切于點
相切于點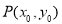
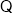
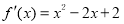 ∴
∴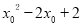
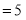 ,解得
,解得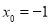 或
或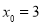
代入直線 方程,得切點
方程,得切點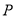 坐標為
坐標為 或
或
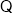 切點
切點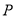 在曲線
在曲線 上,∴
上,∴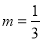 或
或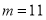
綜上可知,切點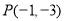 ,
,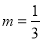 或者切點
或者切點 ,
, 5分
5分
(2)∵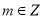 ,∴
,∴ ,設
,設 ,若存在
,若存在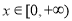 使
使 成立,則只要
成立,則只要 7分
7分

①當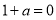 即
即 時
時
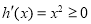 ,
, 是增函數,
是增函數,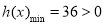 不合題意 8分
不合題意 8分
②若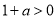 即
即
令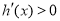 ,得
,得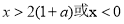 ,∴
,∴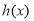 在
在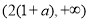 上是增函數
上是增函數
令 ,解得
,解得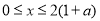 ,∴
,∴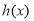 在
在 上是減函數
上是減函數

 ,
, ,解得
,解得 10分
10分
③若 即
即 ,
,
令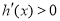 ,解得
,解得
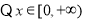 ,∴
,∴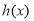 在
在 上是增函數
上是增函數
∴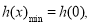
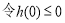 ,不等式無解,∴
,不等式無解,∴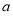 不存在 12分
不存在 12分
綜上可得,實數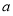 的取值范圍為
的取值范圍為 13分.
13分.
考點:1.導數的幾何意義;2.函數的最值與導數;3.分類討論的思想.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源:2015屆江西贛州四所重點中學高二上學期期末聯考文數學試卷(解析版) 題型:選擇題
已知某幾何體的三視圖如圖所示,其中俯視圖中圓的直徑為4,該幾何體的體積為V1,直徑為4的球的體積為V2,則V1:V2等于( )
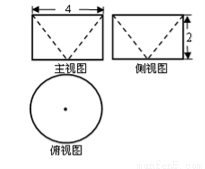
A.1:2
B.2:1
C.1:1
D.1:4
查看答案和解析>>
科目:高中數學 來源:2015屆江西贛州六校高二上學期期末聯考文科數學試卷(解析版) 題型:選擇題
下列說法錯誤的是( )
A.“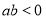 ”是“方程
”是“方程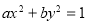 表示雙曲線”的充分不必要條件
表示雙曲線”的充分不必要條件
B.命題“若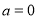 ,則
,則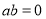 ”的否命題是:“若
”的否命題是:“若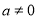 ,則
,則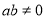 ”
”
C.若命題p:存在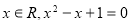 ,則命題p的否定:對任意
,則命題p的否定:對任意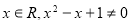
D.若命題“非p”與命題“p或q”都是真命題,那么命題q一定是真命題
查看答案和解析>>
科目:高中數學 來源:2015屆江西省宜春市高二上學期期末統考文科數學試卷(解析版) 題型:填空題
有下列命題:
① 是函數
是函數 的極值點;
的極值點;
②三次函數 有極值點的充要條件是
有極值點的充要條件是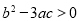 ;
;
③奇函數 在區間
在區間 上是遞增的;
上是遞增的;
④曲線 在
在 處的切線方程為
處的切線方程為 .
.
其中真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源:2015屆江西南昌市四校高二上學期期末聯考文科數學試卷(解析版) 題型:填空題
已知“x-a<1”是 “x2-6x<0”的必要不充分條件,則實數a的取值范圍________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com