
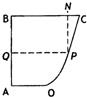
 某地政府為科技興市,欲將如圖所示的一塊不規則的非農業用地規劃建成一個矩形的高科技工業園區.已知AB⊥BC,OA∥BC,且AB=BC=4km,AO=2km,曲線段OC是以點O為頂點且開口向上的拋物線的一段.如果要使矩形的相鄰兩邊分別落在AB,BC上,且一個頂點落在曲線段OC上.問:應如何規劃才能使矩形工業園區的用地面積最大?并求出最大的用地面積(精確到0.1km2).
某地政府為科技興市,欲將如圖所示的一塊不規則的非農業用地規劃建成一個矩形的高科技工業園區.已知AB⊥BC,OA∥BC,且AB=BC=4km,AO=2km,曲線段OC是以點O為頂點且開口向上的拋物線的一段.如果要使矩形的相鄰兩邊分別落在AB,BC上,且一個頂點落在曲線段OC上.問:應如何規劃才能使矩形工業園區的用地面積最大?并求出最大的用地面積(精確到0.1km2).  解:以O為原點,OA所在直線為x軸建立直角坐標系(如圖)
解:以O為原點,OA所在直線為x軸建立直角坐標系(如圖)| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 32 |
| 9 |
| 8 |
| 3 |
| 32 |
| 9 |
| 256 |
| 27 |
| 2 |
| 3 |
| 8 |
| 3 |
| 32 |
| 9 |
| 32 |
| 9 |
| 8 |
| 3 |


科目:高中數學 來源: 題型:
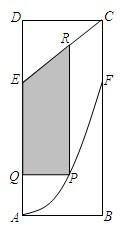 某地政府為科技興市,欲在如圖所示的矩形ABCD的非農業用地中規劃出一個高科技工業園區(如圖中陰影部分),形狀為直角梯形QPRE(線段EQ和RP為兩個底邊),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A為頂點、AD為對稱軸的拋物線段.試求該高科技工業園區的最大面積.
某地政府為科技興市,欲在如圖所示的矩形ABCD的非農業用地中規劃出一個高科技工業園區(如圖中陰影部分),形狀為直角梯形QPRE(線段EQ和RP為兩個底邊),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A為頂點、AD為對稱軸的拋物線段.試求該高科技工業園區的最大面積.查看答案和解析>>
科目:高中數學 來源: 題型:
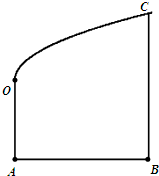 某地政府為科技興市,欲將如圖所示的一塊不規則的非農業用地規劃成一個矩形高科技工業園區.已知AB⊥BC,DA∥BC且AB=BC=2AD=4km,曲線段OC是以點O為頂點且開口向右的拋物線的一段.
某地政府為科技興市,欲將如圖所示的一塊不規則的非農業用地規劃成一個矩形高科技工業園區.已知AB⊥BC,DA∥BC且AB=BC=2AD=4km,曲線段OC是以點O為頂點且開口向右的拋物線的一段.查看答案和解析>>
科目:高中數學 來源: 題型:
 某地政府為科技興市,欲在如圖所示的矩形ABCD的非農業用地中規劃出一個高科技工業園區(如圖中陰影部分),形狀為直角梯形QPRE(線段EQ和RP為兩個底邊),已知AB=2km,BC=6km,AE=BF=4km其中曲線段AF是以A為頂點、AD為對稱軸的拋物線的一部分.分別以直線AB,AD為x軸和y軸建立平面直角坐標系.
某地政府為科技興市,欲在如圖所示的矩形ABCD的非農業用地中規劃出一個高科技工業園區(如圖中陰影部分),形狀為直角梯形QPRE(線段EQ和RP為兩個底邊),已知AB=2km,BC=6km,AE=BF=4km其中曲線段AF是以A為頂點、AD為對稱軸的拋物線的一部分.分別以直線AB,AD為x軸和y軸建立平面直角坐標系.查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省南京師大附中高三(上)12月學情反饋數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com