
 的圖象有三個不同的交點,求實數m的取值范圍.
的圖象有三個不同的交點,求實數m的取值范圍.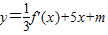 的圖象有三個不同的交點,轉化為方程
的圖象有三個不同的交點,轉化為方程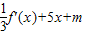 有三個不相等的實根,進一步轉化為函數g(x)=f(x)-
有三個不相等的實根,進一步轉化為函數g(x)=f(x)-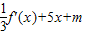 的圖象與x軸有三個不同的交點,于是利用函數導數可得新函數g(x)的極值,通過判斷極值的符號可得結論.
的圖象與x軸有三個不同的交點,于是利用函數導數可得新函數g(x)的極值,通過判斷極值的符號可得結論.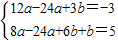 即
即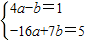 解得a=1,b=3,
解得a=1,b=3,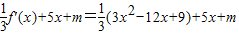 =x2+x+3+m,
=x2+x+3+m,| x | 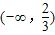 |  | 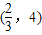 | 4 | (4,+∞) |
| g'(x) | + | - | + | ||
| g(x) | ↗ | 極大值 | ↘ | 極小值 | ↗ |
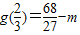 ,極小值為g(4)=-16-m.y=f(x)的圖象與
,極小值為g(4)=-16-m.y=f(x)的圖象與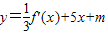 的圖象有三個不同交點,則有:
的圖象有三個不同交點,則有: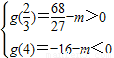 解得
解得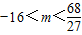 .(12分)
.(12分)

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
| 1 | 3 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省德州市樂陵一中高三(上)期末數學復習訓練試卷17(解析版) 題型:解答題
 的圖象有三個不同的交點,求實數m的取值范圍.
的圖象有三個不同的交點,求實數m的取值范圍.查看答案和解析>>
科目:高中數學 來源:2011年貴州省黔東南州凱里一中高考數學預測試卷1(文科)(解析版) 題型:解答題
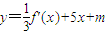 的圖象有三個不同的交點,求實數m的取值范圍.
的圖象有三個不同的交點,求實數m的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com