Question

下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(噸)與相應的生產能耗y(噸標準煤)的幾組對照數據.

x	3	4	5	6
y	2.5	3	4	4.5

(1)請畫出上表數據的散點圖;

(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程y=;

(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(2)求出的線性回歸方程預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?

(參考數值:3×2.5+4×3+5×4+6×4.5=66.5)

(文)已知某幾何體的俯視圖是如圖8所示的矩形,正視圖(或稱主視圖)是一個底邊長為8、高為4的等腰三角形,側視圖(或稱左視圖)是一個底邊長為6、高為4的等腰三角形.

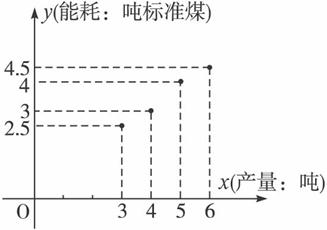
圖8

(1)求該幾何體的體積V;

(2)求該幾何體的側面積S.

Answer 1

答案：分析:本小題主要考查最小二乘法求線性回歸方程、統計量等基礎知識,以及數據處理能力、運算求解能力、應用意識.

解：(1)由題設所給數據,可得散點圖如上圖.

(2)由對照數據,計算得:=86,

=4.5,=3.5,

已知=66.5,所以由最小二乘法確定的回歸方程的系數為

=0.7,=3.5-0.7×4.5=0.35.

因此,所求的線性回歸方程為y=0.7x+0.35.

(3)由(2)的回歸方程及技改前生產100噸甲產品的生產能耗,得降低的生產能耗為90-(0.7×100+0.35)=19.65(噸標準煤).

(文)分析:本小題主要考查三視圖、幾何體體積、等腰三角形性質、三角形面積等基礎知識,以及空間想象能力、運算求解能力.

解：由題設可知幾何體是一個高為4的四棱錐,其底面是長、寬分別為8和6的矩形,正側面及其相對側面均為底邊長為8、高為h₁的等腰三角形,左、右側面均為底邊長為6、高為h₂的等腰三角形,如上圖.

(1)幾何體的體積為V=·S_矩形·h=×6×8×4=64.

(2)正側面及相對側面底邊上的高為h₁==5.

左、右側面的底邊上的高為h₂=.故幾何體的側面面積為

S=2·(×8×5+×6×)=40+2.