
解:由3=e2=1+(![]() )2,得b2=2a2,
)2,得b2=2a2,
雙曲線方程設為![]() =1 ①
=1 ①
設直線l的方程為y=x+m,代入①,得:
2x2-(x+m)2=2a2,即:x2-2mx-(m2+2a2)=0
設P(x1,y1),Q(x2,y2),
則x1+x2=2m,x1·x2=-m2-2a2.
y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2
=-m2-2a2+2m2+m2=2(m2-a2).
∴-3=![]() =x1x2+y1y2=m2-4a2,
=x1x2+y1y2=m2-4a2,
∴4a2-m2-3=0 ②
∵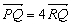 ∴點R分
∴點R分![]() 所成的比為3,點R的坐標為(0,m),則:
所成的比為3,點R的坐標為(0,m),則:
m=![]() +m
+m
∴x1=-3x2,代入x1+x2=2m,得
x1=3m,x2=-m,
代入x1·x2=-m2-2a2,得-3m2=-m2-2a2,
∴m2=a2
代入②得a2=1,從而m=±1
∴直線l的方程為y=x±1,雙曲線的方程為x2-![]() =1
=1


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
. |
| OP |
. |
| OQ |
. |
| PR |
. |
| RQ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 的橢圓C:
的橢圓C: +
+ =1(a>b>0)交于P、Q兩點,直線l與y軸交于點R,且
=1(a>b>0)交于P、Q兩點,直線l與y軸交于點R,且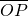 •
•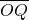 =-3,
=-3, =3
=3 ,求直線l和橢圓C的方程.
,求直線l和橢圓C的方程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com