
設函數f(x)=|2x-1|+|2x-3|,x∈R
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若 的定義域為R,求實數m的取值范圍.
的定義域為R,求實數m的取值范圍.
科目:高中數學 來源: 題型:解答題
設函數 的定義域是
的定義域是 ,對于任意的
,對于任意的 ,有
,有 ,且當
,且當 時,
時, .
.
(1)求 的值;
的值;
(2)判斷函數的奇偶性;
(3)用函數單調性的定義證明函數 為增函數;
為增函數;
(4)若 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
我國是水資源較貧乏的國家之一,各地采用價格調控等手段來達到節約用水的目的,某市每戶每月用水收費辦法是:水費=基本費+超額費+定額損耗費.且有如下兩條規定:
①若每月用水量不超過最低限量 立方米,只付基本費10元加上定額損耗費2元;
立方米,只付基本費10元加上定額損耗費2元;
②若用水量超過 立方米時,除了付以上同樣的基本費和定額損耗費外,超過部分每立方米加付
立方米時,除了付以上同樣的基本費和定額損耗費外,超過部分每立方米加付 元的超額費.
元的超額費.
解答以下問題:(1)寫出每月水費 (元)與用水量
(元)與用水量 (立方米)的函數關系式;
(立方米)的函數關系式;
(2)若該市某家庭今年一季度每月的用水量和支付的費用如下表所示:
| 月份 | 用水量(立方米) | 水費(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
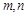 的值.
的值.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=ax2+bx+1(a,b為實數),x∈R,F(x)=
(1)若f(-1)=0,且函數f(x) ≥0的對任意x屬于一切實數成立,求F(x)的表達式;
(2)在 (1)的條件下,當x∈[-2,2]時,g(x)=f(x)-kx是單調函數,求實數k的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 對任意
對任意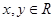 ,都有
,都有 ,當
,當 時,
時,
(1)求證: 是奇函數;
是奇函數;
(2)試問:在 時
時  ,
, 是否有最大值?如果有,求出最大值,如果沒有,說明理由.
是否有最大值?如果有,求出最大值,如果沒有,說明理由.
(3)解關于x的不等式
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com