
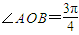 ,求m的最大值.
,求m的最大值.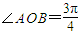 ,所以tan∠AOB=-1,即tan(∠AOM+∠BOM)=-1
,所以tan∠AOB=-1,即tan(∠AOM+∠BOM)=-1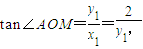 ,
,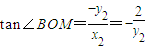 ,
,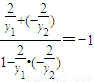 ,
,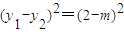 ,
,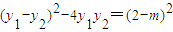 ,所以
,所以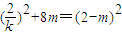 ,即
,即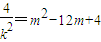 ,
,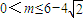 .
.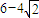 .…(12分)
.…(12分)

科目:高中數學 來源: 題型:
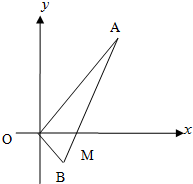 如圖,線段AB過x軸正半軸上一點M(m,0)(m>0),端點A、B到x軸距離之積為2m,以x軸為對稱軸,過A、O、B三點作拋物線.
如圖,線段AB過x軸正半軸上一點M(m,0)(m>0),端點A、B到x軸距離之積為2m,以x軸為對稱軸,過A、O、B三點作拋物線.| 2π | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
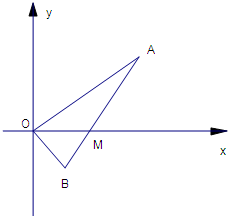 (理)線段AB過x軸正半軸上一點M(m,0)(m>0),端點A、B到x軸的距離之積為3m.以x軸為對稱軸,過A、O、B作拋物線,
(理)線段AB過x軸正半軸上一點M(m,0)(m>0),端點A、B到x軸的距離之積為3m.以x軸為對稱軸,過A、O、B作拋物線,| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3π | 4 |
查看答案和解析>>
科目:高中數學 來源:2013屆江西省高二第二學期第一次月考理科數學 題型:解答題
(12分)如圖,線段AB過x軸正半軸上一定點M(m,0),端點A、B到x軸的距離之積為2m,以x軸為對稱軸,過A、O、B三點作拋物線,求該拋物線的方程。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com