
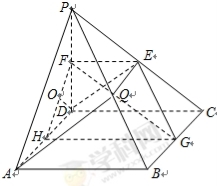
如圖,在四棱錐 中,
中, 是正方形,
是正方形, 平面
平面 ,
, ,
, 分別是
分別是 的中點.
的中點.

(1)在線段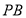 上確定一點
上確定一點 ,使
,使 平面
平面 ,并給出證明;
,并給出證明;
(2)證明平面 平面
平面 ,并求出
,并求出 到平面
到平面 的距離.
的距離.
(1)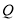 為線段
為線段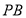 中點時,
中點時,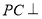 平面
平面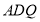 ;(2)
;(2)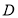 到
到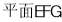 的距離為
的距離為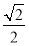 .
.
【解析】
試題分析:
(1)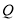 為線段
為線段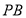 中點,連接
中點,連接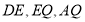 ,可得出
,可得出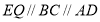 ,所以
,所以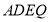 為平面四邊形,先證
為平面四邊形,先證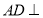 平面
平面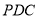 ,所以
,所以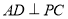 ,又三角形
,又三角形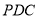 為等腰直角三角形,
為等腰直角三角形,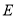 為斜邊中點,所以
為斜邊中點,所以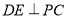 .即可得結論
.即可得結論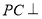 平面
平面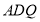 ;
;
(2)根據線線垂直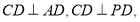 可得線面垂直
可得線面垂直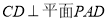 ,
,
進而推出面面垂直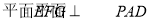 .
.
取所以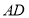 中點所以
中點所以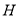 ,證明
,證明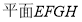 即為
即為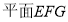 ,因為
,因為  ,在平面
,在平面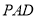 內,作
內,作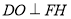 ,垂足為
,垂足為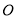 ,則
,則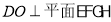 ,
, 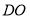 即為
即為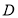 到
到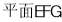 的距離,在三角形
的距離,在三角形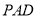 中,
中,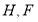 為
為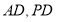 中點,
中點,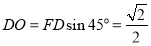 ,即
,即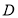 到
到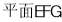 的距離為
的距離為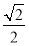 (12分)
(12分)
試題解析:(1) 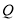 為線段
為線段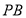 中點時,
中點時,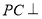 平面
平面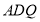 .
.
取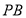 中點
中點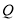 ,連接
,連接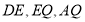 ,
,
由于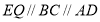 ,所以
,所以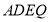 為平面四邊形,
為平面四邊形,
由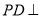 平面
平面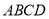 ,得
,得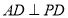 ,
,
又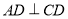 ,
,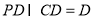 ,所以
,所以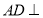 平面
平面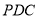 ,
,
所以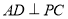 ,
,
又三角形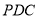 為等腰直角三角形,
為等腰直角三角形,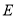 為斜邊中點,所以
為斜邊中點,所以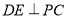 ,
,
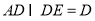 ,所以
,所以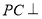 平面
平面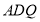 . (5分)
. (5分)
(2)因為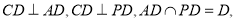 所以
所以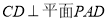 .
.
又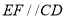 ,所以
,所以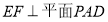 ,所以
,所以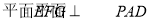 .
.
取所以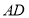 中點所以
中點所以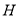 ,連接所以
,連接所以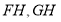 ,則
,則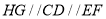 ,
,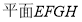 即為
即為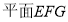 ,
,
在平面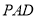 內,作
內,作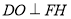 ,垂足為
,垂足為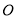 ,則
,則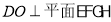 ,
,
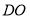 即為
即為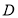 到
到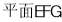 的距離,
的距離,
在三角形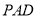 中,
中,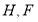 為
為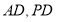 中點,
中點,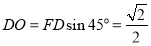 ,
,
即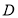 到
到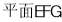 的距離為
的距離為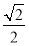 (12分)
(12分)
考點:本題考查線線、線面垂直的判斷和性質,可通過線線垂直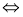 線面垂直
線面垂直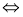 面面垂直的等價轉化方法;
面面垂直的等價轉化方法;
點到平面的距離,可先做垂線,在解三角形.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源:2016屆福建省高一上學期期末數學試卷(解析版) 題型:填空題
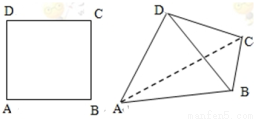
如圖,將邊長為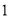 的正方形
的正方形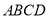 沿對角線
沿對角線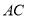 折起,使得平面
折起,使得平面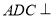 平面
平面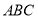 ,在折起后形成的三棱錐
,在折起后形成的三棱錐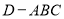 中,給出下列三個命題:
中,給出下列三個命題:
①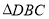 是等邊三角形;②
是等邊三角形;②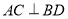 ;③三棱錐
;③三棱錐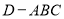 的體積是
的體積是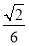 ;④AB與CD所成的角是60°。其中正確命題的序號是 .(寫出所有正確命題的序號)
;④AB與CD所成的角是60°。其中正確命題的序號是 .(寫出所有正確命題的序號)
查看答案和解析>>
科目:高中數學 來源:2016屆甘肅天水一中高一上學期必修一第一學段考試數學試卷(解析版) 題型:填空題
某種商品進貨價每件50元,據市場調查,當銷售價格(每件x元)在 時,每天售出的件數
時,每天售出的件數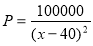 ,當銷售價格定為 元時所獲利潤最多.
,當銷售價格定為 元時所獲利潤最多.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com