
已知橢圓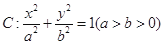 的離心率為
的離心率為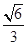 ,短軸一個端到右焦點的距離為
,短軸一個端到右焦點的距離為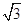 .
.
(Ⅰ)求橢圓C的方程:
(Ⅱ)設直線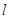 與橢圓C交于A、B兩點,坐標原點O到直線
與橢圓C交于A、B兩點,坐標原點O到直線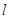 的距離為
的距離為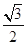 ,求△AOB面積的最大值.
,求△AOB面積的最大值.
(Ⅰ) 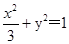 .
.
(Ⅱ) 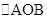 面積取最大值
面積取最大值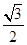 .
.
解析試題分析:(Ⅰ)屬于橢圓的基本題型.通過建立 的方程組,求得橢圓方程為
的方程組,求得橢圓方程為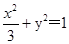 .
.
(Ⅱ)解答本小題,應注意討論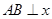 軸和當
軸和當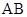 與
與 軸不垂直的兩種情況.在
軸不垂直的兩種情況.在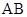 與
與 軸不垂直設直線
軸不垂直設直線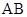 的方程為
的方程為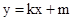 .利用坐標原點
.利用坐標原點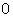 到直線
到直線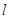 的距離為
的距離為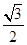 ,建立
,建立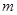 的方程.通過將直線方程與橢圓方程聯立,應用韋達定理、弦長公式,得到
的方程.通過將直線方程與橢圓方程聯立,應用韋達定理、弦長公式,得到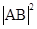 .應用均值定理得到
.應用均值定理得到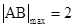 .
.
試題解析:(Ⅰ)設橢圓的半焦距為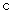 ,依題意,離心率為
,依題意,離心率為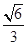 ,短軸一個端到右焦點的距離為
,短軸一個端到右焦點的距離為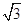 .
.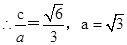 ,
,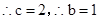 ,∴所求橢圓方程為
,∴所求橢圓方程為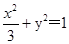 .
.
(Ⅱ)設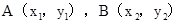 .
.
①當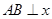 軸時,
軸時,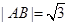 .
.
②當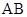 與
與 軸不垂直時,設直線
軸不垂直時,設直線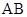 的方程為
的方程為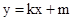 .
.
∵坐標原點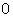 到直線
到直線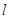 的距離為
的距離為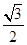 ,
,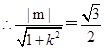 ,
,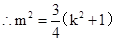
把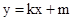 代入橢圓方程,整理得
代入橢圓方程,整理得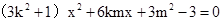 ,
,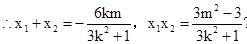
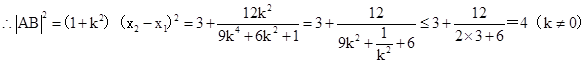
當且僅當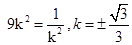 時等號成立,
時等號成立,
當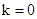 時,
時,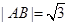 ,
,
綜上所述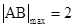 .
.
∴當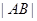 最大時,
最大時,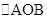 面積取最大值
面積取最大值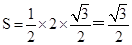 .
.
考點:橢圓方程,直線與橢圓的位置關系,均值定理的應用.


科目:高中數學 來源: 題型:解答題
已知橢圓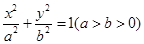 的右準線
的右準線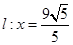 ,離心率
,離心率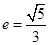 ,
, ,
, 是橢圓上的兩動點,動點
是橢圓上的兩動點,動點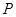 滿足
滿足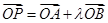 ,(其中
,(其中 為常數).
為常數).
(1)求橢圓標準方程;
(2)當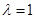 且直線
且直線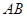 與
與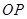 斜率均存在時,求
斜率均存在時,求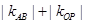 的最小值;
的最小值;
(3)若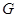 是線段
是線段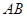 的中點,且
的中點,且 ,問是否存在常數
,問是否存在常數 和平面內兩定點
和平面內兩定點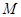 ,
,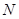 ,使得動點
,使得動點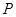 滿足
滿足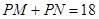 ,若存在,求出
,若存在,求出 的值和定點
的值和定點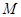 ,
,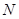 ;若不存在,請說明理由.
;若不存在,請說明理由.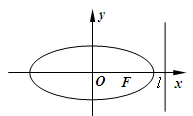
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某化工企業2007年底投入100萬元,購入一套污水處理設備.該設備每年的運轉費用是0.5萬元,此外每年都要花費一定的維護費,第一年的維護費為2萬元,由于設備老化,以后每年的維護費都比上一年增加2萬元.
(1)求該企業使用該設備x年的年平均污水處理費用y(萬元);
(2)為使該企業的年平均污水處理費用最低,該企業幾年后需要重新更換新的污水處理設備?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠擬建一座平面圖為矩形,面積為 的三段式污水處理池,池高為1
的三段式污水處理池,池高為1 ,如果池的四周墻壁的建造費單價為
,如果池的四周墻壁的建造費單價為 元
元 ,池中的每道隔墻厚度不計,面積只計一面,隔墻的建造費單價為
,池中的每道隔墻厚度不計,面積只計一面,隔墻的建造費單價為 元
元 ,池底的建造費單價為
,池底的建造費單價為 元
元 ,則水池的長、寬分別為多少米時,污水池的造價最低?最低造價為多少元?
,則水池的長、寬分別為多少米時,污水池的造價最低?最低造價為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com