(本小題滿分14分)已知⊙
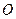
的半徑是
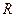
,它的內(nèi)接三角形
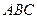
中,有
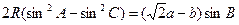
成立,求角
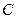
的大小及三角形面積
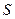
的最大值.
C=
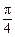
,(S
△ABC)
max =
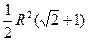
已知等式兩邊同乘以2
R,則有
a2-
c2=
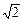 ab
ab-
b2, 2分
即a
2+b
2-c
2=
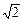
ab, 3分
∴cosC=

.
∴C=
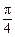
,A+B=
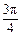
. 6分
∴S
△ABC=
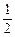
absinC=
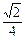
ab=
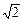
R
2sinA·sinB 8分
=
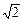
R
2sinA·sin(
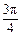
-A)
=
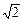
R
2sinA(
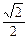
cosA +
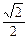
sinA) 9分
= R
2sin
2A + R
2sinA cosA
=
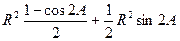
10分
=
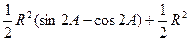
=
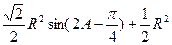
11分

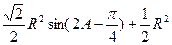
≤
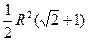
. 12分
即(S
△ABC)
max =
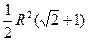
. 14分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題12分)已知A,B,C為
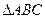
的三個內(nèi)角,向量
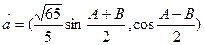
,且
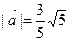
。

(1)求
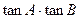
的值;
(2)求C的最大值,并判斷此時
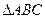
的形狀。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
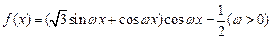
最小正周期為
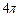
(1)求
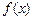
的單調(diào)遞增區(qū)間
(2)在
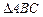
中,角
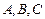
的對邊分別是
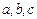
,滿足
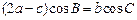
,求函數(shù)
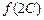
的取值范圍
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
△ABC中,
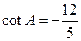
,則
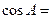
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
過
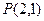
作直線L與x軸正半軸、y軸的正半軸分別交于A、B兩點,設
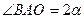
(O為坐標原點),當
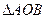
的周長的最小時,
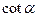
=
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
本小題8分
在
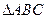
中,角
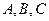
所對的邊分別為
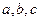
。
(1)若
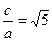
,且
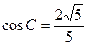
,求
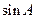
的值。
(2)
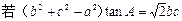
,求
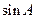
的值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在

中,

為銳角,角

所對應的邊分別為

,且

,

。
(Ⅰ)求

的值;
(Ⅱ)若

,求

的值。
查看答案和解析>>

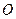 的半徑是
的半徑是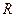 ,它的內(nèi)接三角形
,它的內(nèi)接三角形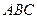 中,有
中,有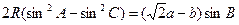 成立,求角
成立,求角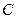 的大小及三角形面積
的大小及三角形面積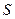 的最大值.
的最大值.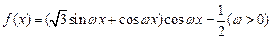 最小正周期為
最小正周期為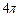
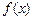 的單調(diào)遞增區(qū)間
的單調(diào)遞增區(qū)間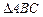 中,角
中,角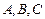 的對邊分別是
的對邊分別是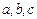 ,滿足
,滿足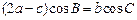 ,求函數(shù)
,求函數(shù)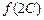 的取值范圍
的取值范圍