Question

已知|a.|=3,b=(2,3),試分別解答下面兩個問題:

(1)若a.⊥b,求a;

(2)若a∥b,求a.

Answer 1

活動:對平面中的兩向量a=(x₁,y₁)與b=(x₂,y₂),要讓學生在應用中深刻領悟其本質屬性,向量垂直的坐標表示x₁x₂+y₁y₂=0與向量共線的坐標表示x₁y₂-x₂y₁=0很容易混淆,應仔細比較并熟記,當難以區分時,要從意義上鑒別,兩向量垂直是a·b=0,而共線是方向相同或相反.教師可多加強反例練習,多給出這兩種類型的同式變形訓練.

解:(1)設a=(x,y),由|a.|=3且a⊥b,

得

解得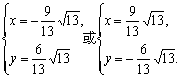

∴a=(a=

(2)設a=(x,y),由|a|=3且a∥b,得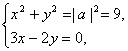

解得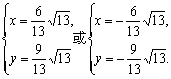

∴aa

點評:本題主要考查學生對公式的掌握情況,學生能熟練運用兩向量的坐標運算來判斷垂直或者共線,也能熟練地進行公式的逆用,利用已知關系來求向量的坐標.