
(1)求雙曲線C的離心率e的取值范圍;
(2)若直線l經(jīng)過(guò)雙曲線C的右焦點(diǎn)F與雙曲線C交于P、Q兩點(diǎn),并且滿足![]() =
=![]()
![]() ,求雙曲線C的方程.
,求雙曲線C的方程.
(文)已知F1、F2分別為橢圓C:![]() =1(a>b>0)的左、右焦點(diǎn),直線l:y=2x+5與橢圓C交于兩點(diǎn)P1、P2,已知橢圓C的中心O關(guān)于直線l的對(duì)稱點(diǎn)恰好落在橢圓C的左準(zhǔn)線上.
=1(a>b>0)的左、右焦點(diǎn),直線l:y=2x+5與橢圓C交于兩點(diǎn)P1、P2,已知橢圓C的中心O關(guān)于直線l的對(duì)稱點(diǎn)恰好落在橢圓C的左準(zhǔn)線上.
(1)求橢圓C的左準(zhǔn)線的方程;
(2)如果![]() a2是
a2是![]() 與
與![]() 的等差中項(xiàng),求橢圓C的方程.
的等差中項(xiàng),求橢圓C的方程.
答案:(理)解:(1)把y=x+m代入曲線![]() =1中,得b2x2-2(x+m)2-2b2=0,整理得(b2-2)x2-4mx-2(m2+b2)=0,當(dāng)b2=2,m=0時(shí)直線與雙曲線無(wú)交點(diǎn),這和直線與雙曲線恒有公共點(diǎn)矛盾,∴b2≠2.∴e≠
=1中,得b2x2-2(x+m)2-2b2=0,整理得(b2-2)x2-4mx-2(m2+b2)=0,當(dāng)b2=2,m=0時(shí)直線與雙曲線無(wú)交點(diǎn),這和直線與雙曲線恒有公共點(diǎn)矛盾,∴b2≠2.∴e≠![]() .
.
當(dāng)b2≠2時(shí),直線與雙曲線恒有公共點(diǎn)?Δ=16m2+8(b2-2)(m2+b2)≥0恒成立,即b4+b2(m2-2)≥0恒成立,
∵b2>0,∴b2+(m2-2)≥0.∴b2≥2-m2.∵e2=![]() =
=![]() ≥
≥![]() ,m∈R,
,m∈R,
∴(![]() )最大=2.∴e2≥2,∴e≥
)最大=2.∴e2≥2,∴e≥![]() .綜上所述,e∈(
.綜上所述,e∈(![]() ,+∞).
,+∞).
(2)設(shè)F(c,0),則直線l:y=x-c,將x=y+c代入雙曲線方程中,得b2(y+c)2-2y2-2b2=0,
整理得(b2-2)y2+2cb2y+b2c2-2b2=0,設(shè)兩交點(diǎn)為P(x1,y1),Q(x2,y2),
則y1+y2=![]() ,y1y2=
,y1y2=![]() ,∵
,∵![]() ,∴y2=5y1.
,∴y2=5y1.
∴6y1=![]() ,5y12=
,5y12=![]() .消去y1,得
.消去y1,得![]() .
.
∵b2>0且c2-2=b2,∴![]() =
=![]() .∴b2=7.∴所求雙曲線C的方程為
.∴b2=7.∴所求雙曲線C的方程為![]() =1.
=1.
(文)解:(1)設(shè)O關(guān)于l的對(duì)稱點(diǎn)為(x0,y0),
∴ 解之,得x0=-4.
解之,得x0=-4.
∴橢圓C的左準(zhǔn)線的方程為x=-4.
(2)設(shè)P1(x1,y1),P2(x2,y2),F1(-c,0),F2(c,0),∴![]() =(x1+c,y1),
=(x1+c,y1),![]() =(x2-c,y2),
=(x2-c,y2),![]() =(c,0).
=(c,0).
∴![]() =c(x1+c),
=c(x1+c),![]() =c(x2-c).依題意,
=c(x2-c).依題意,![]() a2=c(x1+c)+c(x2-c)=c(x1+x2),
a2=c(x1+c)+c(x2-c)=c(x1+x2),
∴x1+x2=![]() ·
·![]() .∵
.∵![]() =4,∴x1+x2=
=4,∴x1+x2=![]() .
.
∴a2=4c.∴b2=4c-c2.∴橢圓C的方程可以化為![]() =1.
=1.
由
![]() (20-c)x2+80x+100-16c+4c2=0.
(20-c)x2+80x+100-16c+4c2=0.
∴x1+x2=![]() .∴
.∴![]() =
=![]() .解之,得c=2.∴a2=8,b2=4.
.解之,得c=2.∴a2=8,b2=4.
∴所求橢圓C的方程為![]() =1.
=1.


 手拉手全優(yōu)練考卷系列答案
手拉手全優(yōu)練考卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
| x2 |
| 2 |
| y2 |
| b2 |
| FP |
| 1 |
| 5 |
| FQ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
A.(1,+∞) B.(![]() ,+∞) C.(
,+∞) C.(![]() ,+∞) D.(2,+∞)
,+∞) D.(2,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
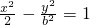 (b>0)恒有公共點(diǎn)
(b>0)恒有公共點(diǎn)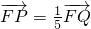 ,求雙曲線C的方程.
,求雙曲線C的方程.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011年黑龍江省哈爾濱六中高考數(shù)學(xué)三模試卷(文科)(解析版) 題型:解答題
 (b>0)恒有公共點(diǎn)
(b>0)恒有公共點(diǎn) ,求雙曲線C的方程.
,求雙曲線C的方程.查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com