
(1)求數列{| a n|}的通項公式;
(2)求向量a n-1與a n的夾角(n≥2);
(3)當k=![]() 時,把a 1, a 2,…, a n,…中所有與a 1共線的向量按原來的順序排成一列,記為b1,b2,…,bn,…,令OBn=b1+b2+…+bn,O為坐標原點,求點列{Bn}的極限點B的坐標.〔注:若點坐標為(tn,sn),且
時,把a 1, a 2,…, a n,…中所有與a 1共線的向量按原來的順序排成一列,記為b1,b2,…,bn,…,令OBn=b1+b2+…+bn,O為坐標原點,求點列{Bn}的極限點B的坐標.〔注:若點坐標為(tn,sn),且![]() tn=t,
tn=t,![]() sn=s,則稱點B(t,s)為點列的極限點〕
sn=s,則稱點B(t,s)為點列的極限點〕
(文)設函數f(x)=5x-6,g(x)=![]() f(x).
f(x).
(1)解不等式g(n)[g(1)+g(2)+…+g(n)]<0(n∈N*);
(2)求h(n)=g(n)[g(1)+g(2)+…+g(n)]-132n(n∈N*)的最小值.
答案:(理)解:(1)| a n|=![]() =
=![]()
=![]() =
=![]() |k||an-1|(n≥2),
|k||an-1|(n≥2),
∴![]() |k|≠0,|a1|=
|k|≠0,|a1|=![]() .
.
∴{|an|}是首項為![]() ,公比為
,公比為![]() |k|的等比數列.∴|an|=
|k|的等比數列.∴|an|=![]() (
(![]() |k|)n-1.
|k|)n-1.
(2)an·an-1=k(xn-1-yn-1,xn-1+yn-1)·(xn-1,yn-1)=k(xn-12+yn-12)=k|an-1|2,
∴cos〈an,an-1〉=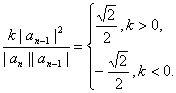
∴當k>0時,〈a,an-1〉=![]() ,當k<0時,〈an,an-1〉=
,當k<0時,〈an,an-1〉=![]() .
.
(3)當k=![]() 時,由(2)知4〈an,an-1〉=π,
時,由(2)知4〈an,an-1〉=π,
∴每相隔3個向量的兩個向量必共線,且方向相反.
∴與向量a1共線的向量為{a1,a5,a9,a13,…}={b1,b2,b3,b4,…}.
記an的單位向量為an0,則a1=|a1|an0,
則an=|an|an0=|a1|(![]() |k|)n-1an0,bn=a4n-3=|a1|(
|k|)n-1an0,bn=a4n-3=|a1|(![]() |k|)4n-4(-1)n-1an0=a1(-4|k|4)n-1=(10,-5)(-
|k|)4n-4(-1)n-1an0=a1(-4|k|4)n-1=(10,-5)(-![]() )n-1.
)n-1.
設![]() =(tn,sn),則tn=10[1+(-
=(tn,sn),則tn=10[1+(-![]() )+(-
)+(-![]() )2+…+(-
)2+…+(-![]() )n-1]=10×
)n-1]=10×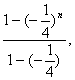 ,
,
∴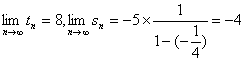 .∴點列{Bn}的極限點B的坐標為(8,-4).
.∴點列{Bn}的極限點B的坐標為(8,-4).
(文)解:(1)g(n)=![]() (5n-6)=2n-12(n∈N*),
(5n-6)=2n-12(n∈N*),
∴g(1)+g(2)+…+g(n)=n2-11n.
解不等式(2n-12)(n2-11n)<0,得6<n<11(n∈N*).
(2)當x∈R時,h(x)=(2x-12)(x2-11x)-132x=2x3-34x2,h′(x)=6x2-68x,
由h′(x)>0,得x<0或x>11![]() ,
,
∵n∈N*,∴1≤n≤11時,h(n)單調遞減,n≥12時,h(n)單調遞增.
當n=11時,h(11)=-1 452,當n=12時,h(12)=-1 440,∴h(n)min=h(11)=-1 452.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| an |
| a1 |
| an |
| an |
| an-1 |
| an |
| 1 |
| 2 |
| a1 |
| a2 |
| an |
| a1 |
| b1 |
| b2 |
| bn |
| OBn |
| b1 |
| b2 |
| bn |
| lim |
| n→∞ |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中數學 來源: 題型:
| an |
| a1 |
| an |
| 1 |
| 2 |
| an |
| a |
| a |
| a |
| a1 |
| a2 |
| an |
| a1 |
| b1 |
| b2 |
. |
| bn |
| OB |
| b1 |
| b2 |
| bn |
| lim |
| n→∞ |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中數學 來源:2010年重慶市一中高一下學期期中考試卷數學 題型:解答題
(12分)已知一列非零向量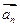 滿足:
滿足: ,[來源:學科網ZXXK]
,[來源:學科網ZXXK] .
.
(1)求證: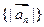 為等比數列;
為等比數列;
( 2)求向量
2)求向量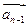 與
與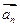 的夾角
的夾角 ;
;
(3)設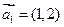 ,記
,記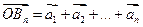 ,設點
,設點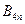 為
為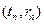 ,則當
,則當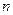 為何值時
為何值時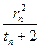 有最小值,并求此最小值.
有最小值,并求此最小值.
查看答案和解析>>
科目:高中數學 來源:2010年重慶市高一下學期期中考試卷數學 題型:解答題
(12分)已知一列非零向量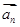 滿足:
滿足: ,[來源:ZXXK]
,[來源:ZXXK]
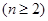 .
.
(1)求證: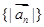 為等比數列;
為等比數列;
(2)求向量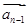 與
與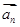 的夾角
的夾角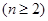 ;
;
(3)設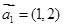 ,記
,記 ,設點
,設點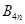 為
為 ,則當
,則當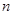 為何值時
為何值時 有最小值,并求此最小值.
有最小值,并求此最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com