Question

（08年華師一附中二次壓軸）過雙曲線的右焦點F₂的直線與右支交于A、B兩點，且線段AF₂、BF₂的長度分別為m、n，m≥n.

(Ⅰ)求證：mn≥1；

(Ⅱ)當直線AB的斜率k∈[，3]時，求的取值范圍.

Answer 1

解析：解法一：(Ⅰ)(1)當直線AB⊥x軸時，則A(，1)，B(，－1)，此時m=n=1，∴mn=1.  

(2)當直線AB不垂直于x軸時，m＞n，設雙曲線的右準線為l，作AA₁⊥l于A₁，作BB₁⊥l于B₁，作BK⊥AA₁于K且交x軸于M

根據雙曲線第二定義有：|AA₁|=m，|BB₁|=n，而F₂到準線l的距離為.

由=得：=，∴2mn=m+n≥，∴mn≥1，∵此時m≠n，∴mn＞1

綜上可知mn≥1

(Ⅱ)設AB：x=ty+，代入雙曲線方程得

∴ 

令，則，且y₁=－y₂代入上面兩式得：

(1－)y₂=－                          ①

                                ②

消去y₂得即         ③

由k∈[，3]有：，綜合③式得3≤+≤4

由＞1得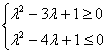

解得∈ 

解法二(Ⅰ)證明：(1)當直線AB斜率不存在時，A(，1)，B(，-1)，∴m=n=1，∴mn=1

(2)當直線AB斜率存在時，設AB：y=k(x－)，A(x₁，y₁)，B(x₂，y₂)

由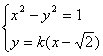得

∵直線AB與雙曲線右支有兩個交點

∴，∴k²－1＞0

∴mn=|a－ex₁|?|a－ex₂|=(ex₁－a)(ex₂－a)=e²x₁x₂－ae(x₁+x₂)+a²==1+＞1

由(1)(2)知:mn≥1

(Ⅱ)解：由題m＞n，則x₁＞x₂

∵k∈[，3]，∴當直線的斜率k逐漸增大時，y₁減小，|y₂|增大，∴逐漸減小

∴(1)當k=時，－4x²+10x－11=0，∴x_1，2=(x₁＞x₂)，∴此時_max=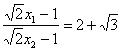 

(2)當k=3時，－8x²+18x－19=0，x_1，2=( x₁＞x₂)，∴此時_min=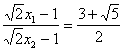

∴的取值范圍是