
某電視臺舉辦了“中華好聲音”大型歌手選秀活動,過程分為初賽、復賽和決賽,經初賽進入復賽的40名選手被平均分成甲、乙兩個班,由組委會聘請兩位導師各負責一個班進行聲樂培訓。下面是根據這40名選手參加復賽時獲得的100名大眾評審的支持票數制成的莖葉圖: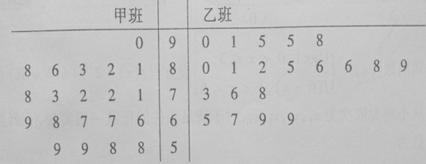
賽制規定:參加復賽的40名選手中,獲得的支持票數排在前5名的選手可進入決賽,若第5名出現并列,則一起進入決賽;另外,票數不低于95票的選手在決賽時擁有“優先挑戰權”。
1、從進入決賽的選手中隨機抽出3名,求其中恰有1名擁有“優先挑戰權”的概率;
2、電視臺決定,復賽票數不低于85票的選手將成為電視臺的“簽約歌手”,請填寫下面的2×2列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成為‘簽約歌手’與選擇的導師有關?
| | 甲班 | 乙班 | 合計 |
| 簽約歌手 | | | |
| 末簽約歌手 | | | |
| 合計 | | | |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
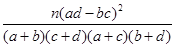 ,其中
,其中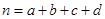
(Ⅰ)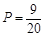 .
.
(Ⅱ)因此在犯錯誤的概率不超過0.025的前提下認為成為‘簽約歌手’與選擇的導師有關.
解析試題分析:(Ⅰ)進入決賽的選手共6名,其中擁有“優先挑戰權”的選手共3名. 2分
為擁有“優先挑戰權”的選手編號為1,2,3,其余3人編號為A,B,C.
被選中3人的編號所有可能的情況共20種,列舉如下:
123,12A,12B,12C,13A,13B,13C,1AB,1AC,1BC,
23A,23B,23C,2AB,2AC,2BC,
3AB,3AC,3BC,
ABC, 4分
其中擁有“優先挑戰權”的選手恰有1名的情況共9種,如下:
1AB,1AC,1BC,2AB,2AC,2BC,3AB,3AC,3BC,
∴所求概率為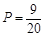 . 6分
. 6分
(Ⅱ)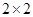 列聯表:
列聯表:
9分 甲班 乙班 合計 簽約歌手 3 10 13 未簽約歌手 17 10 27 合計 20 20 40 
因此在犯錯誤的概率不超過0.025的前提下認為成為‘簽約歌手’與選擇的導師有關. 12分
考點:本題主要考查莖葉圖,古典概型概率的計算,“卡方檢驗”。
點評:典型題,統計中的抽樣方法,頻率直方圖,概率計算及分布列問題,是高考必考內容及題型。古典概型概率的計算問題,關鍵是明確基本事件數,往往借助于“樹圖法”,做到不重不漏。“卡方檢驗”問題,往往直接套用公式加以計算,對照“定值”比較,作出判斷。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某校為了解高三年級不同性別的學生對體育課改上自習課的態度(肯定還是否定),進行了如下的調查研究.全年級共有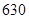 名學生,男女生人數之比為
名學生,男女生人數之比為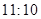 ,現按分層抽樣方法抽取若干名學生,每人被抽到的概率均為
,現按分層抽樣方法抽取若干名學生,每人被抽到的概率均為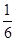 .
.
(1)求抽取的男學生人數和女學生人數;
(2)通過對被抽取的學生的問卷調查,得到如下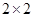 列聯表:
列聯表:
| | 否定 | 肯定 | 總計 |
| 男生 | | 10 | |
| 女生 | 30 | | |
| 總計 | | | |
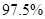 的把握認為態度與性別有關?
的把握認為態度與性別有關?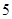 名男生被抽到,其中
名男生被抽到,其中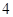 人持否定態度,
人持否定態度, 人持肯定態度;二班有
人持肯定態度;二班有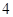 名女生被抽到,其中
名女生被抽到,其中 人持否定態度,
人持否定態度, 人持肯定態度.
人持肯定態度. 人中隨機抽取一男一女進一步詢問所持態度的原因,求其中恰有一人持肯定態度一人持否定態度的概率.
人中隨機抽取一男一女進一步詢問所持態度的原因,求其中恰有一人持肯定態度一人持否定態度的概率.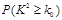 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
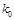 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解學生身高情況,某校以10%的比例對全校700名學生按性別進行分層抽樣調查,測得身高情況的統計圖如下: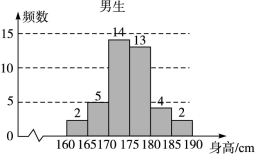
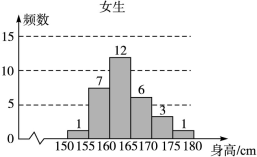
(Ⅰ)估計該校男生的人數;
(Ⅱ)估計該校學生身高在170~185 cm之間的概率;
(Ⅲ)從樣本中身高在180~190 cm之間的男生中任選2人,求至少有1人身高在185~190 cm之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在研究色盲與性別的關系調查中,調查了男性480人,其中有38人患色盲,調查的520名女性中有6人患色盲.
(1)根據以上數據建立一個2×2列聯表;
| | 患色盲 | 不患色盲 | 總計 |
| 男 | | 442 | |
| 女 | 6 | | |
| 總計 | 44 | 956 | 1000 |

| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校從高一年級學生中隨機抽取40名學生,將他們的期中考試數學成績(滿分100分,成績均為不低于40分的整數)分成六段: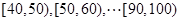 后得到如下圖的頻率分布直方圖.
后得到如下圖的頻率分布直方圖.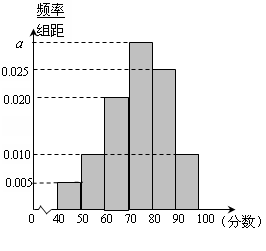
(1)若該校高一年級共有學生 人,試估計該校高一年級期中考試數學成績不低于60分的人數;
人,試估計該校高一年級期中考試數學成績不低于60分的人數;
(2)若從數學成績在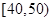 與
與 兩個分數段內的學生中隨機選取兩名學生,求這兩名學生的數學成績之差的絕對值不大于10的概率。
兩個分數段內的學生中隨機選取兩名學生,求這兩名學生的數學成績之差的絕對值不大于10的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品的廣告費用支出 (百萬)與銷售額
(百萬)與銷售額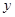 (百萬)之間有如下的對應數據:
(百萬)之間有如下的對應數據:
 | 2 | 4 | 5 | 6 | 8 |
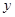 | 30 | 40 | 60 | 50 | 70 |
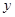 的值.
的值.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(文科)(本小題滿分12分)某高校從參加今年自主招生考試的學生中隨機抽取容量為50的學生成績樣本,得頻率分布表如下:
| 組號 | 分組 | 頻數 | 頻率 |
| 第一組 | [230,235) | 8 | 0.16 |
| 第二組 | [235,240) | ① | 0.24 |
| 第三組 | [240,245) | 15 | ② |
| 第四組 | [245,250) | 10 | 0.20 |
| 第五組 | [250,255] | 5 | 0.10 |
| 合 計 | 50 | 1.00 | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某設備的使用年限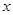 與所支出的總費用
與所支出的總費用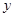 (萬元)有如下的統計資料:
(萬元)有如下的統計資料:
使用年限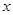 | 1 | 2 | 3 | 4 |
總費用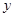 | 1.5 | 2 | 3 | 3.5 |

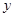 關于
關于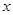 的線性回歸方程
的線性回歸方程 ;
;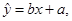 其中
其中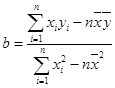 ,
, 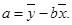
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
在“2012魅力新安江”青少年才藝表演評比活動中,參賽選手成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,可見部分如下圖,據此回答以下問題:
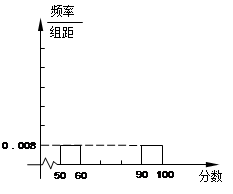
(1)求參賽總人數和頻率分布直方圖中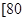 ,
,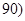 之間的矩形的高,并完成直方圖;
之間的矩形的高,并完成直方圖;
(2)若要從分數在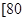 ,
,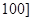 之間任取兩份進行分析,在抽取的結果中,求至少有一份分數在
之間任取兩份進行分析,在抽取的結果中,求至少有一份分數在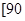 ,
,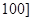 之間的概率.
之間的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com