
(本小題12分)下表提供了工廠技術改造后某種型號設備的使用年限 和所支出的維修費用
和所支出的維修費用 (萬元)的幾組對照數據:
(萬元)的幾組對照數據:
|
|
|
|
|
|
|
|
|
|
|
|
(1)若知道 對
對 呈線性相關關系,請根據上表提供的數據,用最小二乘法求出
呈線性相關關系,請根據上表提供的數據,用最小二乘法求出 關于
關于 的線性回歸方程
的線性回歸方程 ;
;
(2)已知工廠技改前該型號設備使用10年的維修費用為9萬元.試根據(1)求出的線性回歸方程,預測該型號設備技改后使用10年的維修費用比技改前降低多少?
(1)
(2)線性回歸方程為 ;預測該型號設備技改后使用10年的維修費用比技改前降低1.65萬元。
;預測該型號設備技改后使用10年的維修費用比技改前降低1.65萬元。
【解析】
試題分析:(1)根據所給的數據,做出利用最小二乘法需要的四個數據,橫標和縱標的平均數,橫標和縱標的積的和,與橫標的平方和,代入公式求出b的值,再求出a的值,寫出線性回歸方程.
(2)根據上一問做出的線性回歸方程,代入所給的x的值,預報出維修費用,這是一個估計值.
解:(1)
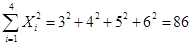


 ;
;
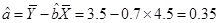
所求的回歸方程為 
(2)當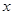 =10時,
=10時,  ,
,
預測該型號設備技改后使用10年的維修費用比技改前降低 (萬元)
(萬元)
答:線性回歸方程為 ;預測該型號設備技改后使用10年的維修費用比技改前降低1.65萬元。
;預測該型號設備技改后使用10年的維修費用比技改前降低1.65萬元。
考點:本試題主要考查了線性回歸分析的應用。本題是一個基礎題.
點評:本題解題的關鍵是利用最小二乘法認真做出線性回歸方程的系數,這是整個題目做對的必備條件。


科目:高中數學 來源:2012-2013學年遼寧省沈陽市高三高考領航考試(一)理科數學試卷(解析版) 題型:解答題
(本小題12分)
某研究機構對高三學生的記憶力x和判斷力y進行統計分析,得下表數據
|
x |
6 |
8 |
10 |
12 |
|
y |
2 |
3 |
5 |
6 |
(1)請畫出上表數據的散點圖;

(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程 ;
;
(3)試根據(II)求出的線性回歸方程,預測記憶力為9的同學的判斷力。
(相關公式: )
)
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高中數學選修2-3 3.2回歸分析練習卷(解析版) 題型:解答題
(本小題12分) 適當飲用葡萄酒可以預防心臟病,下表中的信息是19個發達國家一年中平均每人喝葡萄酒攝取酒精的升數z以及一年中每10萬人因心臟病死亡的人數,
|
國家 |
澳大利亞 |
奧地利 |
比利時 |
加拿大 |
丹麥 |
芬蘭 |
法國 |
冰島 |
爰爾蘭 |
意大利 |
|
x |
2.5 |
3.9 |
2.9 |
2.4 |
2.9 |
0.8 |
9.1 |
0.8 |
0.7 |
7.9 |
|
y |
211 |
167 |
131 |
191 |
220 |
297 |
71 |
221 |
300 |
107 |
|
國家 |
荷蘭 |
新西蘭 |
挪威 |
西班牙 |
瑞典 |
瑞士 |
英國 |
美國 |
德國 |
|
x |
1.8 |
1.9 |
0.8 |
6.5 |
1.6 |
5.8 |
1.3 |
1.2 |
2.7 |
|
y |
167 |
266 |
227 |
86 |
207 |
115 |
285 |
199 |
172 |
(1)畫出散點圖,說明相關關系的方向、形式及強度;
(2)求出每10萬人中心臟病死亡人數,與平均每人從葡萄酒得到的酒精x(L)之間的線性回歸方程.
(3)用(2)中求出的方程來預測以下兩個國家的心臟病死亡率,其中一個國家的成人每年平均從葡萄酒中攝取1L的酒精,另一國則是8 L.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題12分)
某研究機構對高三學生的記憶力x和判斷力y進行統計分析,得下表數據
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;
(3)試根據(II)求出的線性回歸方程,預測記憶力為9的同學的判斷力。
 (相關公式:
(相關公式: )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題12分)
某研究機構對高三學生的記憶力x和判斷力y進行統計分析,得下表數據
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;
(3)試根據(II)求出的線性回歸方程,預測記憶力為9的同學的判斷力。
 (相關公式:
(相關公式: )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com