
 ,
,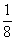 的區(qū)間(a,b),使x0∈(a,b);如果沒有,請說明理由。
的區(qū)間(a,b),使x0∈(a,b);如果沒有,請說明理由。解:(1)由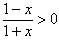 ,得-1<x<1,
,得-1<x<1,
所以函數(shù)f(x)的定義域為(-1,1);
因為f(-x)+f(x)=log2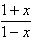 +log2
+log2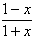 =log2
=log2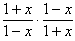 =log21=0,
=log21=0,
所以f(-x)=-f(x),
即f(x)是奇函數(shù);
(2)方程f(x)=log2(x-k)有實根,
也就是方程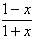 =x-k,即k=x-
=x-k,即k=x-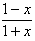 在(-1,1)內有解,
在(-1,1)內有解,
所以實數(shù)k屬于函數(shù)y=x-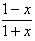 =x+1-
=x+1-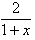 在(-1,1)內的值域。
在(-1,1)內的值域。
令x+1=t,則t∈(0,2),
因為y=t-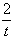 在(0,2)內單調遞增,
在(0,2)內單調遞增,
所以t-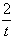 ∈(-∞,1),
∈(-∞,1),
故實數(shù)k的取值范圍是(-∞,1);
(3)設g(x)=f(x)-x-1=log2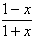 -x-1(-1<x<1),
-x-1(-1<x<1),
用“二分法”逐步探求,先算區(qū)間(-1,1)的中點g(0)=-1<0;
由于g(x)在(-1,1)內單調遞減,
于是再算區(qū)間(-1,0)的中點g(-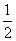 )=log23-
)=log23-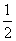 >0;
>0;
然后算區(qū)間(-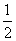 ,0)的中點 g(-
,0)的中點 g(-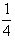 )<0;
)<0;
最后算區(qū)間(-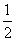 ,-
,-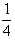 )的中點g(-
)的中點g(-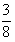 )>0,
)>0,
所以g(- )·g(-
)·g(-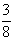 )<0,
)<0,
所以函數(shù)g(x)在區(qū)間(-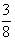 ,-
,-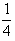 )內有零點x0,
)內有零點x0,
即方程f(x)=x+1在(-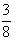 ,-
,-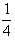 )內有實根x0,
)內有實根x0,
又該區(qū)間長度為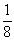 ,
,
因此,所求的一個區(qū)間可以是(-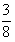 ,-
,-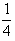 )。
)。
(答案不唯一)


科目:高中數(shù)學 來源: 題型:

 (理)已知函數(shù)f(x)=
(理)已知函數(shù)f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| 1-xp |
| 1+λxp |
| 1 |
| p |
| 1 |
| n |
| n |
 |
| i=1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源:2012年全國普通高等學校招生統(tǒng)一考試理科數(shù)學(江西卷解析版) 題型:解答題
若函數(shù)h(x)滿足
(1)h(0)=1,h(1)=0;
(2)對任意 ,有h(h(a))=a;
,有h(h(a))=a;
(3)在(0,1)上單調遞減。則稱h(x)為補函數(shù)。已知函數(shù)
(1)判函數(shù)h(x)是否為補函數(shù),并證明你的結論;
(2)若存在 ,使得h(m)=m,若m是函數(shù)h(x)的中介元,記
,使得h(m)=m,若m是函數(shù)h(x)的中介元,記 時h(x)的中介元為xn,且
時h(x)的中介元為xn,且 ,若對任意的
,若對任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范圍;
的取值范圍;
(3)當 =0,
=0, 時,函數(shù)y= h(x)的圖像總在直線y=1-x的上方,求P的取值范圍。
時,函數(shù)y= h(x)的圖像總在直線y=1-x的上方,求P的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題

 (理)已知函數(shù)
(理)已知函數(shù)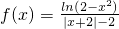 .
.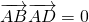 ,求D2+E2-4F的值;
,求D2+E2-4F的值;查看答案和解析>>
科目:高中數(shù)學 來源:2011年上海市普陀區(qū)高考數(shù)學二模試卷(文理合卷)(解析版) 題型:解答題
 .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com