
設函數(shù)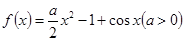 .
.
(1)當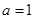 時,求函數(shù)
時,求函數(shù)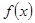 在
在 上的最大值和最小值;
上的最大值和最小值;
(2)若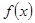 在
在 上為增函數(shù),求正數(shù)
上為增函數(shù),求正數(shù)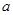 的取值范圍.
的取值范圍.
(1)最小值為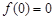 ,最大值為
,最大值為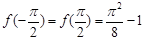 ;(2)
;(2)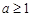 .
.
解析試題分析:(1)當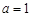 時,
時,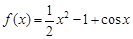 ,其導函數(shù)
,其導函數(shù)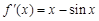 ,易得當
,易得當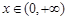 時,
時,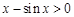 ,即函數(shù)
,即函數(shù)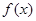 在區(qū)間
在區(qū)間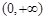 上單調(diào)遞增,又函數(shù)
上單調(diào)遞增,又函數(shù)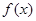 是偶函數(shù),所以函數(shù)
是偶函數(shù),所以函數(shù)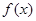 在
在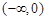 上單調(diào)遞減,
上單調(diào)遞減,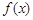 在
在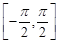 上的最小值為
上的最小值為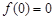 ,最大值為
,最大值為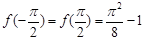 ;
;
(2)由題得: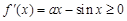 在
在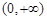 上恒成立,易證
上恒成立,易證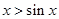 ,若
,若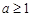 時,則
時,則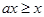 ,所以
,所以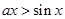 ;若
;若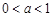 時,易證此時不成立.
時,易證此時不成立.
(1)當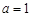 時,
時,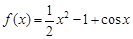 ,
, 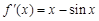 ,
,
令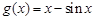 ,則
,則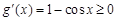 恒成立,
恒成立,
∴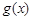 為增函數(shù),
為增函數(shù),
故當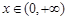 時,
時,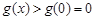
∴當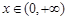 時,
時,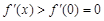 ,∴
,∴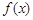 在
在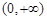 上為增函數(shù),
上為增函數(shù),
又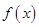 為偶函數(shù),
為偶函數(shù),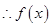 在
在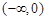 上為減函數(shù),
上為減函數(shù),
∴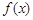 在
在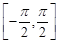 上的最小值為
上的最小值為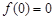 ,最大值為
,最大值為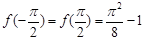 .
.
(2)由題意,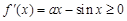 在
在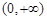 上恒成立.
上恒成立.
(ⅰ)當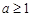 時,對
時,對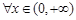 ,恒有
,恒有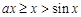 ,此時
,此時 ,函數(shù)
,函數(shù)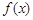 在
在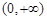 上為增函數(shù),滿足題意;
上為增函數(shù),滿足題意;
(ⅱ)當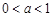 時,令
時,令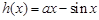 ,
,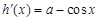 ,由
,由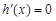 得
得 ,
,
一定 ,使得
,使得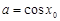 ,且當
,且當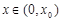 時,
時,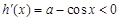 ,
,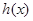 在
在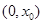 上單調(diào)遞減,此時
上單調(diào)遞減,此時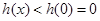 ,即
,即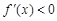 ,所以
,所以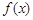 在
在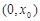 為減函數(shù),這與
為減函數(shù),這與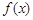 在
在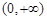 為增函數(shù)矛盾.
為增函數(shù)矛盾.
綜上所述: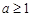 .
.
考點:函數(shù)的最值;函數(shù)的恒成立問題.


 新思維假期作業(yè)寒假吉林大學出版社系列答案
新思維假期作業(yè)寒假吉林大學出版社系列答案科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)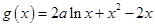 .
.
(1)當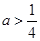 時,討論函數(shù)
時,討論函數(shù)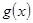 的單調(diào)性;
的單調(diào)性;
(2)當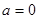 時,在函數(shù)
時,在函數(shù)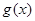 圖象上取不同兩點A、B,設線段AB的中點為
圖象上取不同兩點A、B,設線段AB的中點為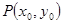 ,試探究函數(shù)
,試探究函數(shù)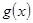 在Q
在Q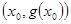 點處的切線與直線AB的位置關系?
點處的切線與直線AB的位置關系?
(3)試判斷當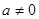 時
時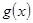 圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
圖象是否存在不同的兩點A、B具有(2)問中所得出的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)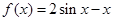 ,
,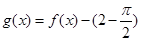 .
.
(1)討論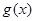 在
在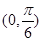 內(nèi)和在
內(nèi)和在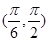 內(nèi)的零點情況.
內(nèi)的零點情況.
(2)設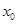 是
是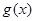 在
在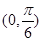 內(nèi)的一個零點,求
內(nèi)的一個零點,求 在
在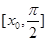 上的最值.
上的最值.
(3)證明對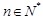 恒有
恒有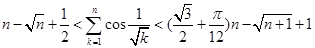 .[來
.[來
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
水庫的蓄水量隨時間而變化,現(xiàn)用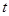 表示時間,以月為單位,年初為起點,根據(jù)歷年數(shù)據(jù),某水庫的蓄水量(單位:億立方米)關于
表示時間,以月為單位,年初為起點,根據(jù)歷年數(shù)據(jù),某水庫的蓄水量(單位:億立方米)關于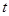 的近似函數(shù)關系式為
的近似函數(shù)關系式為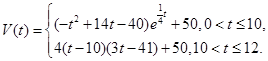
(1)該水庫的蓄求量小于50的時期稱為枯水期.以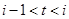 表示第1月份(
表示第1月份(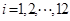 ),同一年內(nèi)哪幾個月份是枯水期?
),同一年內(nèi)哪幾個月份是枯水期?
(2)求一年內(nèi)該水庫的最大蓄水量(取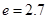 計算).
計算).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com