
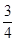 BC,且BG⊥GC,GB=GC=2,E是BC的中點,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中點,PG=4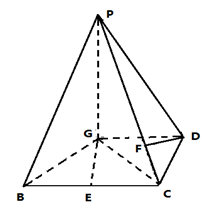
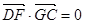 ,
,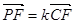 ,求
,求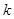 的值.
的值.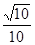 ,(2)
,(2)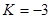
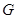 為坐標(biāo)原點,以
為坐標(biāo)原點,以 所在直線分別為
所在直線分別為 軸建立空間直角坐標(biāo)系。根據(jù)已知條件得點的坐標(biāo),再得向量的坐標(biāo)。用向量數(shù)量積公式求向量
軸建立空間直角坐標(biāo)系。根據(jù)已知條件得點的坐標(biāo),再得向量的坐標(biāo)。用向量數(shù)量積公式求向量 所成角的余弦值,但應(yīng)注意空間兩異面直線所成的角為銳角或直角,所以兩異面
所成角的余弦值,但應(yīng)注意空間兩異面直線所成的角為銳角或直角,所以兩異面 和
和 所成角的余弦值為向量
所成角的余弦值為向量 所成角的余弦值的絕對值。(2)根據(jù)題意設(shè)
所成角的余弦值的絕對值。(2)根據(jù)題意設(shè) ,根據(jù)
,根據(jù)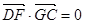 ,可得
,可得 的值,根據(jù)比例關(guān)系即可求得
的值,根據(jù)比例關(guān)系即可求得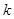 的值。法二:普通方法。(1)根據(jù)異面直線所成角的定義可過
的值。法二:普通方法。(1)根據(jù)異面直線所成角的定義可過 點作
點作 //
//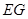 交
交 于
于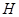 ,則
,則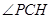 (或其補(bǔ)角)就是異面直線
(或其補(bǔ)角)就是異面直線 與
與 所成的角. 因為
所成的角. 因為 //
//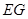 且
且 //
// ,則四邊形
,則四邊形 為平行四邊形,則
為平行四邊形,則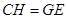 ,
, ,故可在
,故可在 中用余弦定理求
中用余弦定理求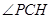 。(2)由
。(2)由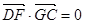 可得
可得 ,過
,過 作
作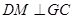 ,
,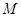 為垂足。易得證
為垂足。易得證 平面
平面 ,可得
,可得 ,從而易得證
,從而易得證 //
// ,可得
,可得 ,即可求
,即可求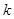 的值。
的值。 點為原點建立空間直角坐標(biāo)系
點為原點建立空間直角坐標(biāo)系 ,
,
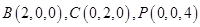 故
故

 與
與 所成角的余弦值為
所成角的余弦值為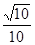 .
.
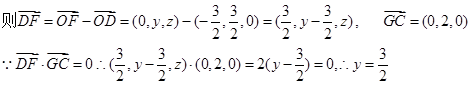
 內(nèi)過
內(nèi)過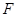 點作
點作 ,
,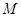 為垂足,則
為垂足,則
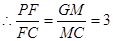 ,∴
,∴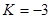
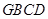 內(nèi),過
內(nèi),過 點作
點作 //
//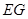 交
交 于
于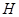 ,連結(jié)
,連結(jié)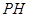 ,則
,則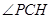 (或其補(bǔ)角)就是異面直線
(或其補(bǔ)角)就是異面直線 與
與 所成的角.
所成的角. 
 中,
中,
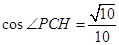
 與
與 所成角的余弦值為
所成角的余弦值為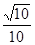 .
.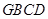 內(nèi),過
內(nèi),過 作
作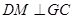 ,
,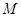 為垂足,連結(jié)
為垂足,連結(jié) ,又因為
,又因為

 平面
平面 ,
, ∴
∴
 平面
平面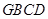 ,∴
,∴ 平面
平面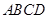 ∴
∴ //
//
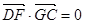 得
得 ,∴
,∴
 ,∴
,∴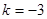 .
.

 名師金手指領(lǐng)銜課時系列答案
名師金手指領(lǐng)銜課時系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
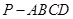 中,底面
中,底面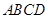 是邊長為1的菱形,
是邊長為1的菱形,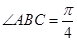 ,
,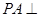 底面
底面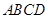 ,
,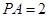 ,
,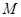 為
為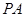 的中點,
的中點,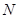 為
為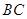 的中點,
的中點,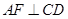 于
于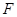 ,如圖建立空間直角坐標(biāo)系.
,如圖建立空間直角坐標(biāo)系.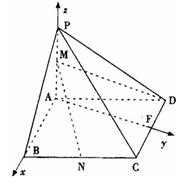
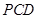 的一個法向量并證明
的一個法向量并證明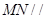 平面
平面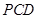 ;
;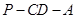 的余弦值.
的余弦值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
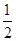 BC,∠ABC=60°,N是BC的中點,將梯形ABCD繞AB旋轉(zhuǎn)90°,得到梯形ABC′D′(如圖).
BC,∠ABC=60°,N是BC的中點,將梯形ABCD繞AB旋轉(zhuǎn)90°,得到梯形ABC′D′(如圖).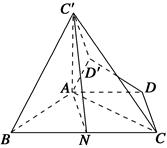
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
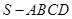 中,底面
中,底面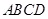 為平行四邊形,側(cè)面
為平行四邊形,側(cè)面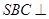 面
面 ,已知
,已知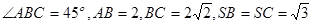
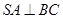 ;
;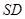 與面
與面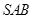 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| n |
| a |
A.若l⊥α,則
| B.若l∥α,則
| ||||||||
C.若
| D.若
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| a |
| b |
| a |
| b |
| OA |
| OB |
| OC |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| A.①② | B.①③ | C.②③ | D.①②③ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
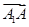 +
+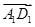 +
+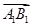 )2=3
)2=3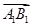 2;②
2;②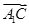 ·(
·(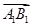 -
-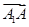 )=0;③向量
)=0;③向量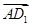 與向量
與向量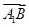 的夾角是60°;④正方體ABCD-A1B1C1D1的體積為|
的夾角是60°;④正方體ABCD-A1B1C1D1的體積為|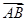 ·
·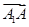 ·
·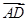 |.其中正確命題的序號是________.
|.其中正確命題的序號是________.查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com