
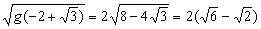
(1)若折痕所在直線的斜率為k,試寫出折痕所在直線的方程;
(2)求折痕的長的最大值.
解:(1)①當k=0時,此時A點與D點重合,折痕所在的直線方程y=![]() .
.
②當k≠0時,設A點落在線段DC上的點A′(x0,1),
(0≤x0≤2),則直線OA′的斜率kOA′=![]() ,
,
∵折痕所在直線垂直平分OA′,
∴kOA′·k=-1,
∴![]() ·k=-1,∴x0=-k.
·k=-1,∴x0=-k.
又∵折痕所在的直線與OA′的交點坐標(線段OA′的中點)
為M(![]() ,
, ![]() ),
),
∴折痕所在的直線方程y-![]() =k(x+
=k(x+![]() ),即y=kx+
),即y=kx+![]() +
+![]() ,
,
由①②得折痕所在的直線方程為:y=kx+![]() +
+![]() (-2≤k≤0).
(-2≤k≤0).
(2)折痕所在的直線與坐標軸的交點坐標為E(0,![]() ),F(
),F(![]() ,0).
,0).
由(1)知,k=-x0,
∵0≤x0≤2,∴-2≤k≤0,
設折痕長度為d,所在直線的傾斜角為θ,
①當k=0時,此時A點與D點重合,折痕的長為2;
②當-2≤k<0時,
設a=![]() ,b=
,b=![]() ,
,
0<a≤|AB|=2時,l與線段AB相交,此時-2≤k≤-2+![]() ,
,
a>|AB|=2時,l與線段BC相交,此時-2+![]() <k<0,
<k<0,
0<b≤1時,l與線段AD相交,此時-1≤k<0,
b>1時,l與線段DC相交,此時-2≤k<-1,
∴將k所在的區間分為3個子區間:
a.當-2≤k<-1時,折痕所在的直線l與線段DC、AB相交,
折痕的長d=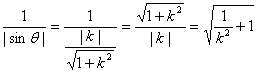 ,
,
∴![]() ≤d<
≤d<![]() ,
,
b.當-1≤k≤-2+![]() 時,折痕所在的直線l與線段AD、AB相交,
時,折痕所在的直線l與線段AD、AB相交,
折痕的長d=![]() ,
,
令g′(x)≥0,即k3+![]() ≥0,
≥0,
即2k6+3k4-1≤0,
即(k2+1)2(k2-![]() )≤0.
)≤0.
∵-1≤k≤-2+![]() ,
,
∴解得![]() ≤k≤-2+
≤k≤-2+![]() ,
,
令g′(x)≤0,解得-1≤k≤![]() ,
,
故當-1≤k≤![]() 時,g(x)是減函數;當
時,g(x)是減函數;當![]() ≤k≤-2+
≤k≤-2+![]() 時,g(x)是增函數,
時,g(x)是增函數,
∵g(-1)=2,g(-2+![]() )=4(8-4
)=4(8-4![]() ),
),
∴g(-1)<g(-2+![]() ),
),
∴當k=-2+![]() 時,g(-2+
時,g(-2+![]() )=4(8-4
)=4(8-4![]() ).
).
d=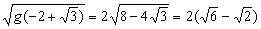 .
.
∴當-1≤k≤-2+![]() 時,d≤
時,d≤![]() ;
;
c.當-2+![]() <k<0時,折痕所在的直線l與線段AD、BC相交,
<k<0時,折痕所在的直線l與線段AD、BC相交,
折痕的長d=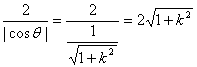 ,
,
∴2<l<![]() ,即2<l<2(
,即2<l<2(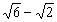 ),
),
綜上所述得,當k=-2+3時,折痕的長有最大值,最大值為2(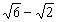 ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| π | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com