
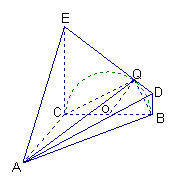
已知幾何體A―BCED的三視圖如圖所示,其中俯視圖和側視圖都是腰長為4的等腰直角三角形,正視圖為直角梯形.
(1)求此幾何體的體積V的大小;
(2)求異面直線DE與AB所成角的余弦值;
 (3)試探究在DE上是否存在點Q,使得AQ
(3)試探究在DE上是否存在點Q,使得AQ![]() BQ并說明理由(一、二、五中必做,其它學校選做).
BQ并說明理由(一、二、五中必做,其它學校選做).
解析:(1)由該幾何體的三視圖知![]() 面
面![]() ,且EC=BC=AC=4 ,BD=1,
,且EC=BC=AC=4 ,BD=1,
 ∴
∴![]()
∴![]() .
.
即該幾何體的體積V為16. -----------3分
(2)解法1:過點B作BF//ED交EC于F,連結AF,
則∠FBA或其補角即為異面直線DE與AB所成的角.-------5分
在△BAF中,∵AB=![]() ,BF=AF=
,BF=AF=![]() .
.
∴![]()
![]() .
.
即異面直線DE與AB所成的角的余弦值為![]() .------------------------------------------7分
.------------------------------------------7分
 解法2:以C為原點,以CA,CB,CE所在直線為x,y,z軸建立空間直角坐標系.
解法2:以C為原點,以CA,CB,CE所在直線為x,y,z軸建立空間直角坐標系.
則A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4)
∴![]() ,∴
,∴![]()
∴異面直線DE與AB所成的角的余弦值為![]() .
.
(3)解法1:在DE上存在點Q,使得AQ![]() BQ.--------------------------------------------------8分
BQ.--------------------------------------------------8分
取BC中點O,過點O作OQ⊥DE于點Q,則點Q滿足題設.
連結EO、OD,在Rt△ECO和Rt△OBD中
∵![]()
![]() ∴
∴![]() ∽
∽![]() ∴
∴![]()
 ∵
∵![]() ∴
∴![]() ∴
∴![]() .-----------------10分
.-----------------10分
∵![]() ,
,![]()
∴![]()
∴以O為圓心、以BC為直徑的圓與DE相切.切點為Q
∴![]()
∵![]() 面
面![]() ,
,![]() 面
面![]() ∴
∴![]() ∴
∴![]() 面
面![]()
∵![]() 面ACQ w.w.w.k.s.5.u.c.o.m
面ACQ w.w.w.k.s.5.u.c.o.m ![]()
∴![]() .-------------------------------------------------------------------------12分
.-------------------------------------------------------------------------12分
解法2: 以C為原點,以CA,CB,CE所在直線為x,y,z軸建立空間直角坐標系.
設滿足題設的點Q存在,其坐標為(0,m,n),則![]()
![]() ,
,![]()
∵AQ![]() BQ ∴
BQ ∴![]() ----------------------------①
----------------------------①
∵點Q在ED上,∴存在![]()
![]() 使得
使得![]()
∴![]()
![]() -----------②
-----------②
②代入①得![]() ,解得
,解得![]()
∴滿足題設的點Q存在,其坐標為![]()


科目:高中數學 來源: 題型:
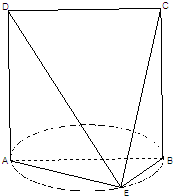 如圖,已知四邊形ABCD是邊長為4cm的正方形,直線AD垂直于以AB為直徑的圓所在的平面,點E是該圓上異于A,B的一點,連接AE、BE、DE、CE.
如圖,已知四邊形ABCD是邊長為4cm的正方形,直線AD垂直于以AB為直徑的圓所在的平面,點E是該圓上異于A,B的一點,連接AE、BE、DE、CE.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知四邊形ABCD是邊長為4cm的正方形,直線AD垂直于以AB為直徑的圓所在的平面,點E是該圓上異于A,B的一點,連接AE、BE、DE、CE.
如圖,已知四邊形ABCD是邊長為4cm的正方形,直線AD垂直于以AB為直徑的圓所在的平面,點E是該圓上異于A,B的一點,連接AE、BE、DE、CE.查看答案和解析>>
科目:高中數學 來源:2009-2010學年廣東省廣州市海珠區高一(上)學業質量監測數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com