
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 8 |


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| x |
| 2 |
| 2k+1 |
| 3 |
| π |
| 6 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| x |
| 2 |
| 2k+1 |
| 3 |
| π |
| 6 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖北省黃石市大冶市華中學校高三數學滾動訓練(三)(解析版) 題型:填空題
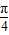 ,
,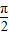 ),則f(sinθ)>f(cosθ);
),則f(sinθ)>f(cosθ);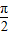 ;
;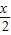 -1,則f(x+π)=f(x)對x∈R恒成立;
-1,則f(x+π)=f(x)對x∈R恒成立;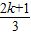 πx-
πx-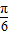 )(k∈N*)在區間[a,a+3]上的值
)(k∈N*)在區間[a,a+3]上的值 出現的次數不小于4次,又不多于8次,則k可以取2和3.
出現的次數不小于4次,又不多于8次,則k可以取2和3. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com