一個口袋內有4個不同的紅球,6個不同的白球.
(1)從中任取4個球,紅球個數不少于白球個數的取法有多少種?
(2)若取一個紅球記2分,取一個白球記1分,從中任取5個球,使總分不少于7的取法
科目：高中數學 來源： 題型：解答題
為了解學生身高情況，某校以10%的比例對全校700名學生按性
別進行分層抽樣調查，測得身高情況的統計圖如下：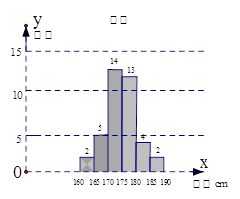 
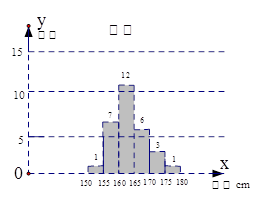
（1）估計該校男生的人數；
（2）估計該校學生身高在170～185㎝之間的概率；
（3）從樣本中身高在165～180㎝之間的女生中任選2人，求至少有1人身高在170～180㎝之間的概率；
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知
的展開式中，某一項的系數是它前一項系數的2倍，而又等于它后一項系數的
（Ⅰ）求展開后所有項的系數之和及所有項的二項式系數之和；
（Ⅱ）求展開式中的有理項．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
設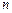
是給定的正整數，有序數組
同時滿足下列條件：
①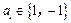 
,
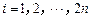； ②對任意的
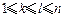,都有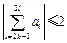
．
（1）記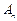
為滿足“對任意的
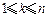，都有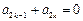
”的有序數組的個數，求；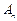
（2）記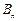
為滿足“存在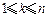，使得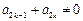
”的有序數組的個數，求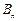
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（滿分12分）從1，3，5，7，9中任取三個數字，從2，4，6，8中任取兩個數字，可以組成多少：（列出式子并用數字給出最后答案）
（1）無重復數字的五位數；
（2）萬位、百位和個位數字是奇數的無重復數字的五位數；
（3）千位和十位數字只能是奇數的無重復數字的五位數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
種取法; 第二類有3個紅球,則有
種取法; 第三類有2個紅球,則有
種取法;各根據加法原理共有1+24+90=115種不同的取法.
種不同的取法.
(
N*)展開式中，前三項的二項式系數和是
，求：
的值；
(
N*)展開式中，前三項的二項式系數和是
，求：（Ⅰ）
的值；（Ⅱ）展開式中的常數項．
的展開式的二項式系數之和比(a＋b)2n的展開式的系數之和小240，求
；
；
； 
；