
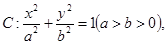 動直線
動直線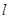 與橢圓
與橢圓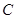 只有一個公共點
只有一個公共點 ,且點
,且點 在第一象限.
在第一象限.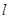 的斜率為
的斜率為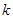 ,用
,用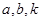 表示點
表示點 的坐標;
的坐標;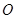 的直線
的直線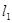 與
與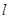 垂直,證明:點
垂直,證明:點 到直線
到直線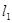 的距離的最大值為
的距離的最大值為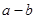 .
. 的坐標為
的坐標為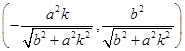 ;(2)詳見解析.
;(2)詳見解析.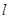 的斜率為
的斜率為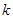 ,用
,用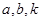 表示點
表示點 的坐標,由已知橢圓
的坐標,由已知橢圓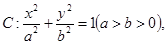 動直線
動直線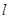 與橢圓
與橢圓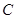 只有一個公共點
只有一個公共點 ,可設出直線
,可設出直線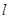 的方程為
的方程為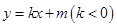 ,結合橢圓方程,得
,結合橢圓方程,得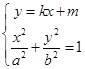 ,消去
,消去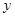 得,
得,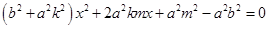 ,令
,令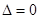 ,得
,得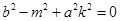 ,即
,即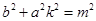 ,代入原式得點
,代入原式得點 的坐標為
的坐標為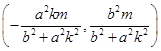 ,再由點
,再由點 在第一象限,得
在第一象限,得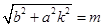 ,可得點
,可得點 的坐標為
的坐標為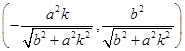 ;(2)點
;(2)點 到直線
到直線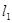 的距離的最大值為
的距離的最大值為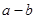 ,由直線
,由直線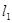 過原點
過原點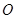 且與
且與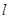 垂直,得直線
垂直,得直線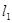 的方程為
的方程為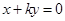 ,利用點到直線距離公式可得
,利用點到直線距離公式可得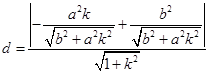 ,即
,即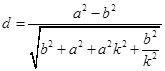 ,由式子特點,需消去
,由式子特點,需消去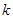 即可,注意到
即可,注意到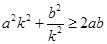 ,代入即可證明.
,代入即可證明.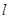 的方程為
的方程為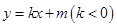 ,由
,由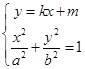 ,消去
,消去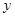 得,
得,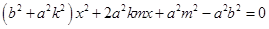 ,由于直線
,由于直線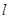 與橢圓
與橢圓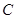 只有一個公共點
只有一個公共點 ,故
,故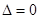 ,即
,即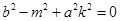 ,解得點
,解得點 的坐標為
的坐標為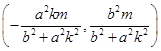 ,由點
,由點 在第一象限,故點
在第一象限,故點 的坐標為
的坐標為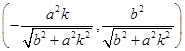 ;
;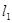 過原點
過原點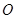 ,且與
,且與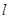 垂直,故直線
垂直,故直線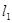 的方程為
的方程為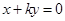 ,所以點
,所以點 到直線
到直線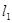 的距離
的距離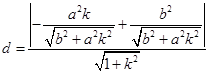 ,整理得
,整理得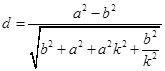 ,因為
,因為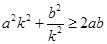 ,所以
,所以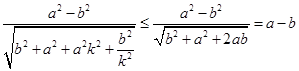 ,當且僅當
,當且僅當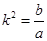 時等號成立,所以點
時等號成立,所以點 到直線
到直線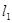 的距離的最大值為
的距離的最大值為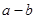 .
.

 小學數(shù)學口算題卡脫口而出系列答案
小學數(shù)學口算題卡脫口而出系列答案 優(yōu)秀生應用題卡口算天天練系列答案
優(yōu)秀生應用題卡口算天天練系列答案 浙江之星課時優(yōu)化作業(yè)系列答案
浙江之星課時優(yōu)化作業(yè)系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
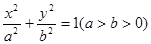 的右焦點為
的右焦點為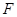 ,
,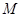 為上頂點,
為上頂點,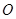 為坐標原點,若△
為坐標原點,若△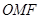 的面積為
的面積為 ,且橢圓的離心率為
,且橢圓的離心率為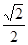 .
.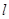 交橢圓于
交橢圓于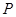 ,
,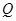 兩點, 且使點
兩點, 且使點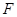 為△
為△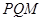 的垂心?若存在,求出直線
的垂心?若存在,求出直線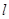 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
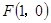 的距離和到直線
的距離和到直線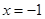 的距離相等.若機器人接觸不到過點
的距離相等.若機器人接觸不到過點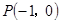 且斜率為
且斜率為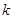 的直線,則
的直線,則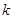 的取值范圍是___________.
的取值范圍是___________.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
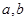 ,定義
,定義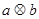 的算法原理如右側程序框圖所示.設
的算法原理如右側程序框圖所示.設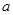 為函數(shù)
為函數(shù)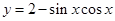 的最大值,
的最大值,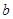 為雙曲線
為雙曲線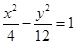 的離心率,則計算機執(zhí)行該運算后輸出的結果是( )
的離心率,則計算機執(zhí)行該運算后輸出的結果是( )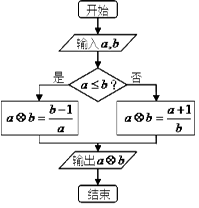
A.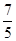 | B.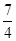 | C.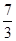 | D.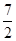 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
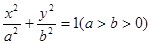 的左右頂點分別為
的左右頂點分別為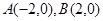 ,離心率
,離心率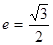 .
.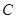 為曲線
為曲線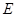 :
: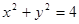 上任一點(
上任一點(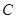 點不同于
點不同于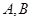 ),直線
),直線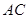 與直線
與直線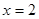 交于點
交于點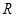 ,
,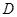 為線段
為線段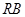 的中點,試判斷直線
的中點,試判斷直線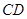 與曲線
與曲線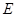 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
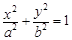 的一個焦點為
的一個焦點為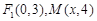
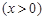 為橢圓C上一點,△MOF2的面積為
為橢圓C上一點,△MOF2的面積為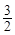 .
.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com