
設 (
( 且
且 ),g(x)是f(x)的反函數.
),g(x)是f(x)的反函數.
(Ⅰ)設關于 的方程求
的方程求 在區間[2,6]上有實數解,求t的取值范圍;
在區間[2,6]上有實數解,求t的取值范圍;
(Ⅱ)當a=e(e為自然對數的底數)時,證明: ;
;
(Ⅲ)當0<a≤時,試比較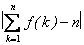 與4的大小,并說明理由.
與4的大小,并說明理由.
[番茄花園1]1.
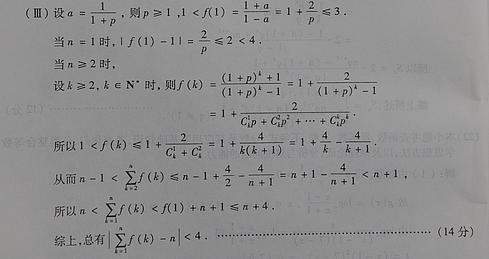
本小題考產函數、反函數、方程、不等式、導數及其應用等基礎知識,考察化歸、分類整合
等數學思想方法,以及推理論證、分析與解決問題的能力.
解:(1)由題意,得ax=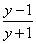 >0
>0
故g(x)=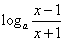 ,x∈(-∞,-1)∪(1,+∞)
,x∈(-∞,-1)∪(1,+∞)
由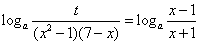 得
得
t=(x-1)2(7-x),x∈[2,6]
則t'=-3x2+18x-15=-3(x-1)(x-5)
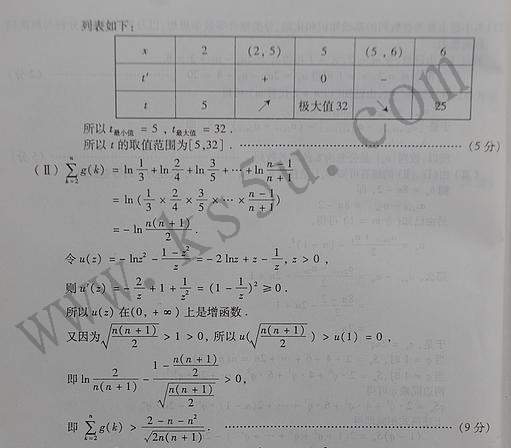
列表如下:
|
x |
2 |
(2,5) |
5 |
(5,6) |
6 |
|
t' |
|
+ |
0 |
- |
|
|
t |
5 |
↗ |
極大值32 |
↘ |
25 |
所以t最小值=5,t最大值=32
所以t的取值范圍為[5,32]……………………………………………………5分
(2) 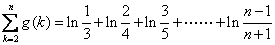
=ln(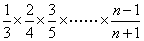 )
)
=-ln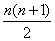
令u(z)=-lnz2-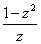 =-2lnz+z-
=-2lnz+z-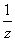 ,z>0
,z>0
則u'(z)=-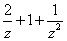 =(1-
=(1-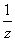 )2≥0
)2≥0
所以u(z)在(0,+∞)上是增函數
又因為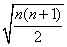 >1>0,所以u(
>1>0,所以u(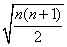 )>u(1)=0
)>u(1)=0
即ln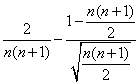 >0
>0
即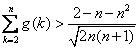 ………………………………………………………………9分
………………………………………………………………9分
(3)設a=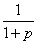 ,則p≥1,1<f(1)=
,則p≥1,1<f(1)=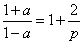 ≤3
≤3
當n=1時,|f(1)-1|=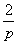 ≤2<4
≤2<4
當n≥2時
設k≥2,k∈N *時,則f(k)=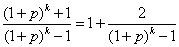
=1+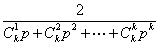
所以1<f(k)≤1+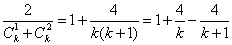
從而n-1<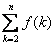 ≤n-1+
≤n-1+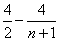 =n+1-
=n+1- <n+1
<n+1
所以n<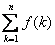 <f(1)+n+1≤n+4
<f(1)+n+1≤n+4
綜上所述,總有|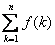 -n|<4
-n|<4
[番茄花園1]22.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com