
 對任意實數
對任意實數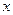 均有
均有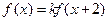 ,其中常數
,其中常數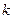 為負數,且
為負數,且 在區間
在區間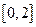 上有表達式
上有表達式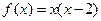 .
.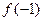 ,
,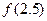 的值;
的值; 在
在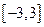 上的表達式,并討論函數
上的表達式,并討論函數 在
在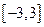 上的單調性;
上的單調性; 在
在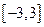 上的最小值與最大值,并求出相應的自變量的取值.
上的最小值與最大值,并求出相應的自變量的取值.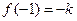 ,
,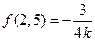
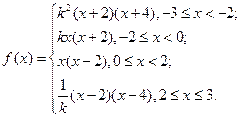
 在
在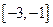 與
與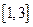 上為增函數,在
上為增函數,在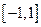 上為減函數;
上為減函數; 而
而 在
在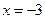 處取得最小值
處取得最小值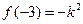 ,在
,在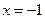 處取得最大值
處取得最大值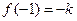 .
.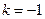 時,
時, 在
在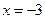 與
與 處取得最小值
處取得最小值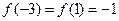 ,在
,在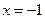 與
與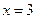 處取得最大值
處取得最大值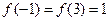 .
.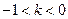 時,
時, 在
在 處取得最小值
處取得最小值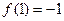 ,在
,在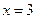 處取得最大值
處取得最大值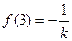 .
.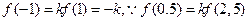 ,
,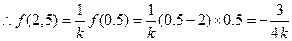 .
. 對任意實數
對任意實數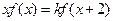 ,
, .
.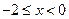 時,
時, ;
; 時,
時,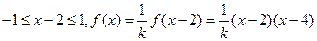 .
.
 在
在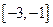 與
與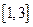 上為增函數,在
上為增函數,在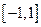 上為減函數;
上為減函數; 在
在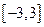 上的單調性可知,
上的單調性可知, 在
在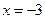 或
或 處取得最小值
處取得最小值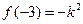 或
或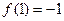 ,而在
,而在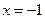 或
或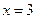 處取得最大值
處取得最大值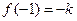 或
或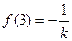 .
. 而
而 在
在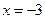 處取得最小值
處取得最小值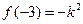 ,在
,在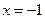 處取得最大值
處取得最大值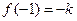 .
.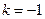 時,
時, 在
在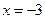 與
與 處取得最小值
處取得最小值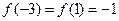 ,在
,在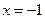 與
與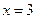 處取得最大值
處取得最大值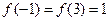 .
.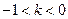 時,
時, 在
在 處取得最小值
處取得最小值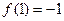 ,在
,在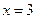 處取得最大值
處取得最大值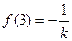 .
.

 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com