
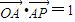 .設
.設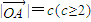 ,
,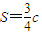 ,并且以O為中心、A為焦點的橢圓經過點P.當
,并且以O為中心、A為焦點的橢圓經過點P.當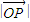 取得最小值時,則此橢圓的方程為 .
取得最小值時,則此橢圓的方程為 .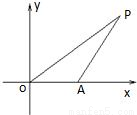
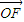 所在直線為x軸建立直角坐標系,
所在直線為x軸建立直角坐標系, =c,P點坐標為(x,y),則
=c,P點坐標為(x,y),則 •
•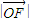 •|y|=
•|y|=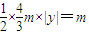 ,即
,即 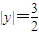 .因為
.因為 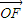 =(c,0),
=(c,0),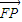 =(x-c,y),
=(x-c,y),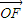 •
•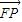 =1,可得
=1,可得 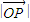 =
=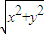 =
=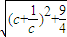 ,設
,設 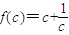 ,判斷知f(c)在[2,+∞)上是增函數;所以當c=2時,f(c)為最小,從而
,判斷知f(c)在[2,+∞)上是增函數;所以當c=2時,f(c)為最小,從而 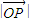 為最小,此時P(
為最小,此時P( 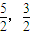 ),最終得到答案.
),最終得到答案.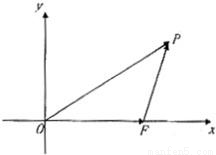 如圖,以O為原點,
如圖,以O為原點,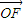 所在直線為x軸建立直角坐標系
所在直線為x軸建立直角坐標系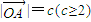 ,
,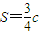 ,
, •
•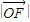 •|y|=
•|y|=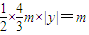 ,∴
,∴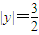
 =(c,0),
=(c,0),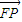 =(x-c,y),
=(x-c,y),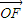 •
•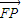 =1
=1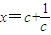
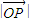 =
=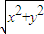 =
=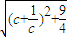
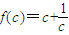 ,當c≥2時,任取c2>c1≥2
,當c≥2時,任取c2>c1≥2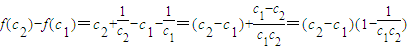
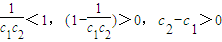
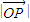 為最小,此時P(
為最小,此時P( 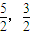 )
)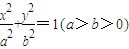 ,則
,則 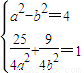 ∴a2=10,b2=6
∴a2=10,b2=6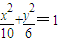 .
.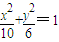 .
.

 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
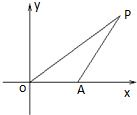 如圖,已知△OAP的面積為S,
如圖,已知△OAP的面積為S,| OA |
| AP |
| OA |
| 3 |
| 4 |
| OP |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com