
已知函數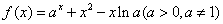 .
.
(Ⅰ)當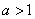 時,求證:函數
時,求證:函數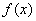 在
在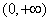 上單調遞增;
上單調遞增;
(Ⅱ)若函數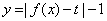 有三個零點,求
有三個零點,求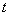 的值;
的值;
(Ⅲ)若存在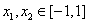 ,使得
,使得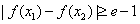 ,試求
,試求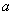 的取值范圍.
的取值范圍.
鹽城市2009/2010學年度高三年級第一次調研考試
數學附加題部分
(本部分滿分40分,考試時間30分鐘)
解:(Ⅰ)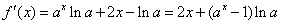 …………………………………3分
…………………………………3分
由于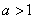 ,故當
,故當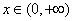 時,
時,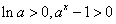 ,所以
,所以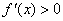 ,
,
故函數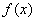 在
在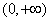 上單調遞增
……………………………………………………………5分
上單調遞增
……………………………………………………………5分
(Ⅱ)當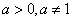 時,因為
時,因為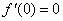 ,且
,且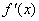 在R上單調遞增,
在R上單調遞增,
故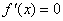 有唯一解
有唯一解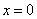 ……………………………………………………………………7分
……………………………………………………………………7分
所以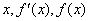 的變化情況如下表所示:
的變化情況如下表所示:
|
x |
|
0 |
|
|
|
- |
0 |
+ |
|
|
遞減 |
極小值 |
遞增 |
又函數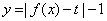 有三個零點,所以方程
有三個零點,所以方程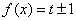 有三個根,
有三個根,
而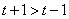 ,所以
,所以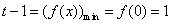 ,解得
,解得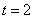 ……………………………11分
……………………………11分
(Ⅲ)因為存在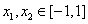 ,使得
,使得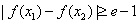 ,
,
所以當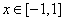 時,
時,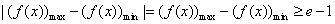 …………12分
…………12分
由(Ⅱ)知,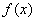 在
在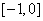 上遞減,在
上遞減,在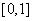 上遞增,
上遞增,
所以當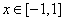 時,
時,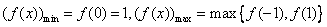 ,
,
而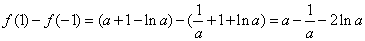 ,
,
記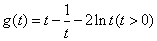 ,因為
,因為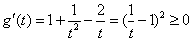 (當
(當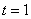 時取等號),
時取等號),
所以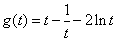 在
在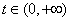 上單調遞增,而
上單調遞增,而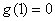 ,
,
所以當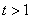 時,
時,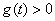 ;當
;當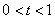 時,
時,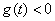 ,
,
也就是當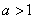 時,
時,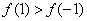 ;當
;當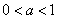 時,
時,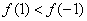 ………………………14分
………………………14分
①當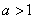 時,由
時,由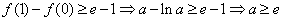 ,
,
②當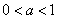 時,由
時,由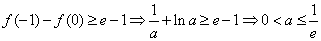 ,
,
綜上知,所求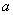 的取值范圍為
的取值范圍為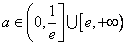 …………………………………………16分
…………………………………………16分


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com