
 ,
, 滿足|
滿足| |=2,|
|=2,| |=1,
|=1, ,
, 的夾角為60°,
的夾角為60°, =2x
=2x +7
+7 ,
, =
= +x
+x ,x∈R.
,x∈R. ,
, 的夾角為鈍角,求x的取值范圍;
的夾角為鈍角,求x的取值范圍; •
• ,求f(x)在[-1,1]上的最大值與最小值.
,求f(x)在[-1,1]上的最大值與最小值.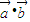 的值,再由
的值,再由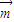 ,
,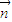 的夾角為鈍角可知
的夾角為鈍角可知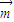 •
•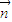 <0,代入即可解題.
<0,代入即可解題.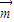 •
•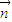 的值確定函數f(x)的解析式,再根據二次函數的單調性求出在[-1,1]上的最大值與最小值.
的值確定函數f(x)的解析式,再根據二次函數的單調性求出在[-1,1]上的最大值與最小值.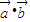 =|a||b|cos60°=2×1×cos60°=1,
=|a||b|cos60°=2×1×cos60°=1,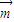 ,
,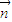 的夾角為鈍角,得
的夾角為鈍角,得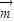 •
•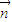 <0,且
<0,且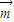 ≠λ
≠λ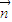
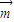 •
•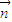 =(2x
=(2x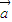 +7
+7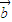 )•(
)•(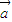 +x
+x )=2x
)=2x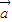 2+2
2+2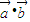 +2x2
+2x2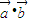 +7
+7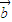 2
2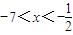 ,
, ≠λ
≠λ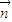
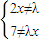 ,解得x≠
,解得x≠
 ;
;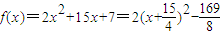 ,f(x)在[-1,1]上單調遞增,
,f(x)在[-1,1]上單調遞增,

 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| b |
| m |
| n |
| m |
| n |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com