
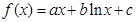 (
(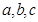 �dz���(sh��))��
�dz���(sh��))��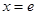 ̎���о����̞�
̎���о����̞�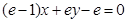 ����
����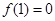 .
.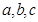 ��ֵ��
��ֵ��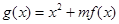 (
(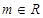 )�څ^(q��)�g
)�څ^(q��)�g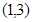 ��(n��i)���dž��{(di��o)����(sh��)����(sh��)��(sh��)
��(n��i)���dž��{(di��o)����(sh��)����(sh��)��(sh��)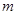 ��ȡֵ������
��ȡֵ������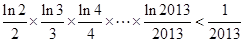 .
.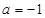 ��
��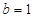 ��
��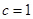 ������(sh��)��(sh��)
������(sh��)��(sh��)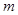 ��ȡֵ������
��ȡֵ������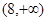 ������ԔҊ(ji��n)������
������ԔҊ(ji��n)������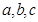 ��ֵ���ɺ���(sh��)
��ֵ���ɺ���(sh��)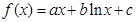 (
(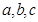 �dz���(sh��))��
�dz���(sh��))��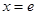 ̎���о����̞�
̎���о����̞�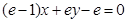 ��ֻ�茦(du��)
��ֻ�茦(du��)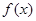 ��(d��o)�����Č�(d��o)��(sh��)��
��(d��o)�����Č�(d��o)��(sh��)�� ̎��ֵ�����о���б�ʣ��@���ܵõ�
̎��ֵ�����о���б�ʣ��@���ܵõ�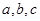 ��һ��(g��)�P(gu��n)ϵʽ����
��һ��(g��)�P(gu��n)ϵʽ����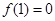 �����뺯��(sh��)�У��ֵõ�
�����뺯��(sh��)�У��ֵõ�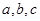 ��һ��(g��)�P(gu��n)ϵʽ����?y��n)�����(g��)����(sh��)��������һ��(g��)�P(gu��n)ϵʽ����ע�
��һ��(g��)�P(gu��n)ϵʽ����?y��n)�����(g��)����(sh��)��������һ��(g��)�P(gu��n)ϵʽ����ע�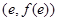 ���о��ϣ��ɴ����о����̵õ�
���о��ϣ��ɴ����о����̵õ�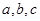 ��һ��(g��)�P(gu��n)ϵʽ����ʽ(li��n)�����̽M���ɣ������}���P(gu��n)�I����
��һ��(g��)�P(gu��n)ϵʽ����ʽ(li��n)�����̽M���ɣ������}���P(gu��n)�I����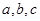 ���P(gu��n)ϵʽ���Ўׂ�(g��)����(sh��)������?gu��)ׂ�(g��)�P(gu��n)ϵʽ������������(sh��)
���P(gu��n)ϵʽ���Ўׂ�(g��)����(sh��)������?gu��)ׂ�(g��)�P(gu��n)ϵʽ������������(sh��)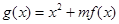 (
(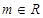 )�څ^(q��)�g
)�څ^(q��)�g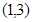 ��(n��i)���dž��{(di��o)����(sh��)�������Č�(d��o)����(sh��)�څ^(q��)�g
��(n��i)���dž��{(di��o)����(sh��)�������Č�(d��o)����(sh��)�څ^(q��)�g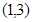 ��(n��i)���������ؓ(f��)����
��(n��i)���������ؓ(f��)����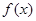 �څ^(q��)�g
�څ^(q��)�g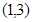 ��(n��i)�ИOֵ�c(di��n)����
��(n��i)�ИOֵ�c(di��n)����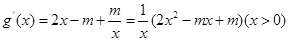 ��ֻҪ
��ֻҪ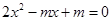 �څ^(q��)�g
�څ^(q��)�g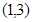 ��(n��i)�н⣬�Ķ��D(zhu��n)������κ���(sh��)���ķֲ���(w��n)�}���փɷN��r���څ^(q��)�g
��(n��i)�н⣬�Ķ��D(zhu��n)������κ���(sh��)���ķֲ���(w��n)�}���փɷN��r���څ^(q��)�g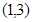 ��(n��i)��һ�⣬�څ^(q��)�g
��(n��i)��һ�⣬�څ^(q��)�g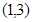 ��(n��i)�Ѓɽ⣬�Y(ji��)�϶��κ���(sh��)�D�Ķ������(sh��)��(sh��)
��(n��i)�Ѓɽ⣬�Y(ji��)�϶��κ���(sh��)�D�Ķ������(sh��)��(sh��)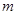 ��ȡֵ�����������C��:
��ȡֵ�����������C��: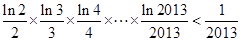 ��ע�
��ע� ��ֻ���C��
��ֻ���C��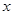 ��
��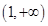 ��
��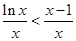 ���ɣ���
���ɣ���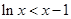 ����
����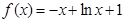 ��ֻ���C��
��ֻ���C��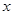 ��
��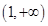 ��
��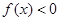 ���ɣ���
���ɣ���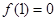 ����
����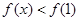 ��ֻ���C
��ֻ���C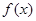 ��
��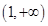 �Ϟ�p����(sh��)���@�������C�������}��(g��u)˼�������֪�R(sh��)�c(di��n)�࣬�W(xu��)��֪�R(sh��)�c(di��n)�ں���һ�𣬵Ĵ_��һ��(g��)���}�����P(gu��n)�}���ã�
�Ϟ�p����(sh��)���@�������C�������}��(g��u)˼�������֪�R(sh��)�c(di��n)�࣬�W(xu��)��֪�R(sh��)�c(di��n)�ں���һ�𣬵Ĵ_��һ��(g��)���}�����P(gu��n)�}���ã�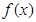 �Ķ��x��?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824022856985525.png" style="vertical-align:middle;" />,
�Ķ��x��?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824022856985525.png" style="vertical-align:middle;" />,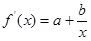 , ��?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824022856970463.png" style="vertical-align:middle;" />��
, ��?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824022856970463.png" style="vertical-align:middle;" />��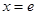 ̎���о����̞�
̎���о����̞�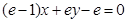 ������
������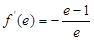 ,��
,��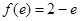 ����
����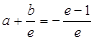 ,��
,��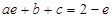 �� ��
�� ��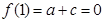 �����
�����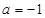 ��
��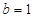 ��
�� ��
��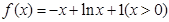 �� ��ˣ�
�� ��ˣ�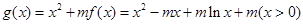 ��
�� 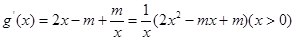 ����
����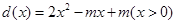 . ��������(d��ng)����(sh��)
. ��������(d��ng)����(sh��)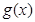 ��
��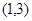 ��(n��i)��һ��(g��)�Oֵ�r(sh��)��
��(n��i)��һ��(g��)�Oֵ�r(sh��)��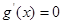 ��
��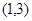 ��(n��i)���҃H��һ��(g��)������
��(n��i)���҃H��һ��(g��)������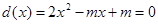 ��
��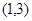 ��(n��i)���҃H��һ��(g��)��������?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824022857313622.png" style="vertical-align:middle;" />����(d��ng)
��(n��i)���҃H��һ��(g��)��������?y��n)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824022857313622.png" style="vertical-align:middle;" />����(d��ng)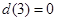 ����
����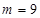 �r(sh��)��
�r(sh��)��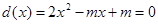 ��
��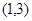 ��(n��i)���҃H��һ��(g��)��
��(n��i)���҃H��һ��(g��)��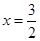 ����(d��ng)
����(d��ng)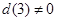 �r(sh��)����(y��ng)��
�r(sh��)����(y��ng)��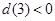 ����
����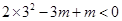 �����
�����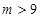 ��������
��������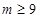 . ��������(d��ng)����(sh��)
. ��������(d��ng)����(sh��)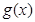 ��
��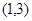 ��(n��i)�Ѓɂ�(g��)�Oֵ�r(sh��)��
��(n��i)�Ѓɂ�(g��)�Oֵ�r(sh��)��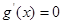 ��
��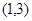 ��(n��i)�Ѓɂ�(g��)���������κ���(sh��)
��(n��i)�Ѓɂ�(g��)���������κ���(sh��)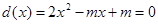 ��
��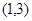 ��(n��i)�Ѓɂ�(g��)���ȸ�������
��(n��i)�Ѓɂ�(g��)���ȸ�������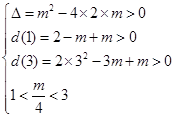 �����
�����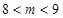 . �C�ϣ���(sh��)��(sh��)
. �C�ϣ���(sh��)��(sh��)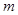 ��ȡֵ������
��ȡֵ������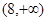 ��
�� 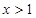 �r(sh��)����
�r(sh��)����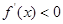 ������
������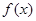 ��
��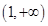 �Ϟ�p����(sh��)����ˮ�(d��ng)
�Ϟ�p����(sh��)����ˮ�(d��ng)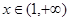 �r(sh��),
�r(sh��),  ����
����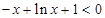 �� ����(d��ng)
�� ����(d��ng)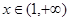 �r(sh��),
�r(sh��), 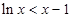 �� ����
�� ����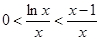 ��(du��)һ��
��(du��)һ��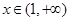 ������������
������������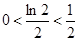 ��
�� 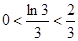 ��
��  �� ����
�� ���� 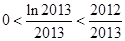 ������
������ 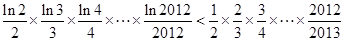 �� ����
�� ����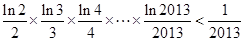 .
. 

 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
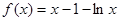
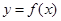 ���c(di��n)
���c(di��n)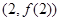 ̎���о����̣�
̎���о����̣�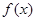 �ĘOֵ��
�ĘOֵ��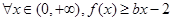 ���������(sh��)��(sh��)
���������(sh��)��(sh��)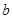 ��ȡֵ����.
��ȡֵ����.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
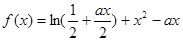
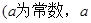 ��0��
��0�� ��һ��(g��)�Oֵ�c(di��n)����
��һ��(g��)�Oֵ�c(di��n)����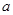 ��ֵ��
��ֵ��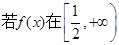 ����������(sh��)����a��ȡֵ����
����������(sh��)����a��ȡֵ���� 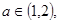 ������
������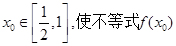 ��
��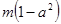 ��������(sh��)��(sh��)m��ȡֵ����
��������(sh��)��(sh��)m��ȡֵ�����鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
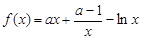
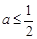 �r(sh��)��ԇӑՓ����(sh��)
�r(sh��)��ԇӑՓ����(sh��)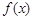 �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�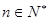 ����
����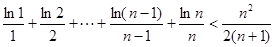 .
.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
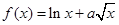
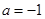 ��
��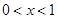 �r(sh��)��
�r(sh��)��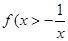 ��
��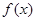 �ڶ��x���(n��i)�����c(di��n)��(g��)��(sh��)�����C����ĽY(ji��)Փ.
�ڶ��x���(n��i)�����c(di��n)��(g��)��(sh��)�����C����ĽY(ji��)Փ.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
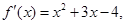 �t
�t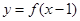 ���{(di��o)�p�^(q��)�g�� ��
���{(di��o)�p�^(q��)�g�� ��A��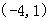 | B��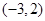 | C��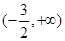 | D��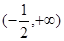 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
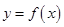 ��
��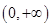 �ϵČ�(d��o)����(sh��)��
�ϵČ�(d��o)����(sh��)��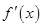 ���Ҳ���ʽ
���Ҳ���ʽ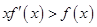 ��������ֳ���(sh��)
��������ֳ���(sh��)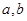 ���M��
���M��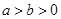 ���t���в���ʽһ���������� .
���t���в���ʽһ���������� .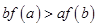 ����
����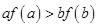 ����
����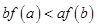 ����
����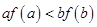 .
.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ����x�}
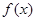 ��(d��o)����(sh��)��
��(d��o)����(sh��)��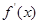 ����(du��)����
����(du��)����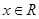 ����
����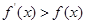 �������t��������
�������t��������A�� | B��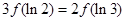 |
C��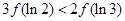 | D��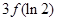 �c �c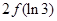 �Ĵ�С���_�� �Ĵ�С���_�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ����Ԕ �}�ͣ�����}
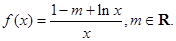
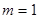 ���Дຯ��(sh��)�ڶ��x���(n��i)�Ć��{(di��o)�ԣ�
���Дຯ��(sh��)�ڶ��x���(n��i)�Ć��{(di��o)�ԣ�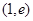 ��(n��i)���ژOֵ����(sh��)��(sh��)m��ȡֵ������
��(n��i)���ژOֵ����(sh��)��(sh��)m��ȡֵ�������鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com