
 的底面
的底面 是矩形,
是矩形, 、
、 分別是
分別是 、
、 的中點,
的中點, 底面
底面 ,
, ,
,
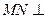 平面
平面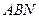
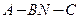 的余弦值
的余弦值
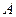 點為原點,
點為原點,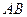 為
為
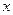 軸,
軸,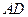
 為
為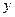 軸,
軸,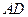 為
為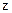 軸的空間直角坐標系,如圖所示.則依題意可知相關各點的坐標分別是:
軸的空間直角坐標系,如圖所示.則依題意可知相關各點的坐標分別是: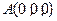 ,
,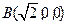 ,
,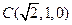 ,
,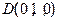 ,
,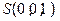 如下圖所示.………………………………………………………
如下圖所示.……………………………………………………… ……………………(2分)
……………………(2分)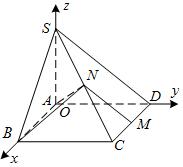
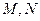 點的坐標分別為
點的坐標分別為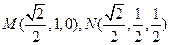 ……………………………
…………………………… ……………(3分)
……………(3分)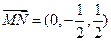 ,
,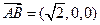 ,
,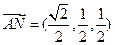 ......................... (4分)
......................... (4分)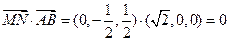 ,所以
,所以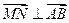 .......................... (6分)
.......................... (6分)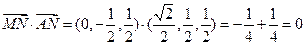 ,所以
,所以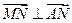 .............. (7分)
.............. (7分)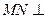 平面
平面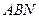 ........................................................... (8分)
........................................................... (8分)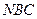 的法向量
的法向量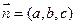 ,則
,則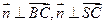 ,........................ (9分)
,........................ (9分)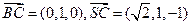
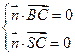
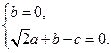 ............................................................. (10分)
............................................................. (10分)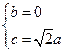
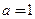 ,則
,則
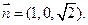
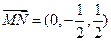 就是平面
就是平面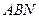 的法向量................................... (11分)
的法向量................................... (11分)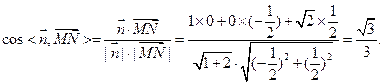 .................... (12分)
.................... (12分)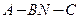 是鈍角二面角........................................ (13分)
是鈍角二面角........................................ (13分)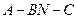 的余弦值為
的余弦值為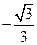 .......................................... (14分)
.......................................... (14分)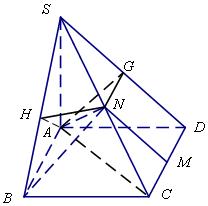
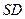 的中點
的中點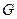 ,連接
,連接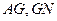 ,則
,則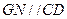 ,又
,又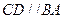 ,所以四點
,所以四點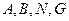 共面.
共面.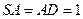 ,且
,且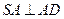 .......... (2分)]
.......... (2分)]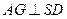 .
.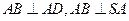 ,
,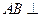 平面
平面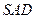 ..................... (4分)
..................... (4分)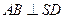
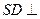 平面
平面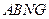 ................... (6分)
................... (6分)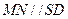
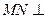 平面
平面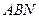 ................... (8分)
................... (8分)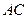 ,則
,則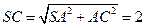
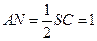 .............................................................. (9分)
.............................................................. (9分)
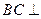 平面
平面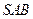 .
.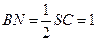 ,且平面
,且平面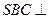 平面
平面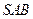 .
.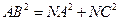 ,所以
,所以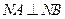 ........................................... (10分)
........................................... (10分)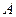 作
作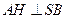 ,垂足為
,垂足為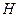 ,則
,則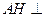 平面
平面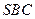 .
.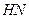 ,則
,則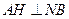 ......................................................... (11分)
......................................................... (11分)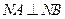 ,
,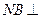 平面
平面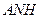 ,
,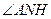 為二面角
為二面角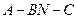 平面角的補角. ....................................... (12分)
平面角的補角. ....................................... (12分)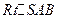 中,
中,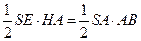 ,所以
,所以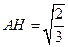 .
.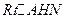 中,
中,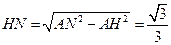
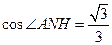 ........................................................... (13分)
........................................................... (13分)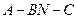 的余弦值為
的余弦值為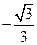 .......................................... (14分)
.......................................... (14分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題: ,
, ,則
,則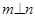 ②若
②若 ,
, ,
, ,則
,則
 ,
, ,則
,則 ④若
④若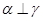 ,
, ,則
,則
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com