
 記
記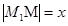 ,n臺機器人送檢時間總和為f(x).
,n臺機器人送檢時間總和為f(x). |
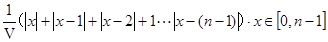 ;(2)x=1;(3)n為偶數時x∈[
;(2)x=1;(3)n為偶數時x∈[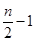 ,
,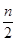 ];n為奇數時
];n為奇數時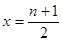 .
.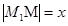 且
且 ,則
,則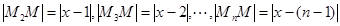 ,從而可得f(x)的表達式;(2)當n=3時,f(x)
,從而可得f(x)的表達式;(2)當n=3時,f(x)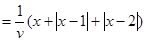
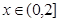 是一個含有絕對值符號的函數,只須采用零點分段討論法,去掉絕對值符號,轉化為一個分段函數,結合函數圖就可求得使f(x)取得最小值對應的x的值;(3)由(1)知f(x)是一個含有多個絕對值符號的函數,再由(2)的經驗,須去掉絕對值符號,所以我們只須設i≤x≤i+1,(0≤i<n-2, i∈Ζ),就可去掉所有的絕對值符號,從而轉化為一個一次函數,其單調性由x系數的正負來確定,討論x系數的正負,并結合n的奇偶性就可求出f(x)取得最小值時,x的取值范圍.
是一個含有絕對值符號的函數,只須采用零點分段討論法,去掉絕對值符號,轉化為一個分段函數,結合函數圖就可求得使f(x)取得最小值對應的x的值;(3)由(1)知f(x)是一個含有多個絕對值符號的函數,再由(2)的經驗,須去掉絕對值符號,所以我們只須設i≤x≤i+1,(0≤i<n-2, i∈Ζ),就可去掉所有的絕對值符號,從而轉化為一個一次函數,其單調性由x系數的正負來確定,討論x系數的正負,并結合n的奇偶性就可求出f(x)取得最小值時,x的取值范圍.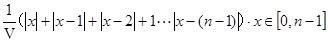 3分
3分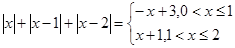
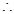 f(x)在x=1處取得最小值
f(x)在x=1處取得最小值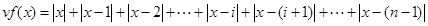
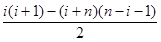
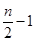 時,f(x)單調遞減:當
時,f(x)單調遞減:當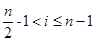 時,f(x)單調遞增
時,f(x)單調遞增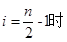 , f(x)為常函數,又f(x)圖象是一條連續不斷的圖象,所以
, f(x)為常函數,又f(x)圖象是一條連續不斷的圖象,所以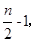 )內單調遞減,在(
)內單調遞減,在(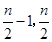 )為常函數,在(
)為常函數,在(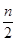 ,n-1)單調遞增,所以當x∈[
,n-1)單調遞增,所以當x∈[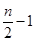 ,
,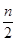 ]時f(x)取得最小值.
]時f(x)取得最小值.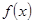 在
在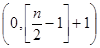 內單調遞減,(
內單調遞減,(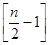 表示
表示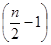 的整數部分),在
的整數部分),在 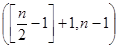 內單調遞增,所以當
內單調遞增,所以當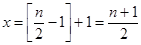 時
時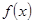 取得最小值 (13分)
取得最小值 (13分)

 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源:不詳 題型:解答題
 是長方形海域,其中
是長方形海域,其中 海里,
海里, 海里.現有一架飛機在該海域失事,兩艘海事搜救船在
海里.現有一架飛機在該海域失事,兩艘海事搜救船在 處同時出發,沿直線
處同時出發,沿直線 、
、 向前聯合搜索,且
向前聯合搜索,且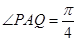 (其中
(其中 、
、 分別在邊
分別在邊 、
、 上),搜索區域為平面四邊形
上),搜索區域為平面四邊形 圍成的海平面.設
圍成的海平面.設 ,搜索區域的面積為
,搜索區域的面積為 .
.
 與
與 的關系式,并指出
的關系式,并指出 的取值范圍;
的取值范圍; 的最大值,并指出此時
的最大值,并指出此時 的值.
的值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com