中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知f1(x)＝Asin(ωx＋)(A＞0，ω＞0，||＜)的部分圖象如下圖所示：

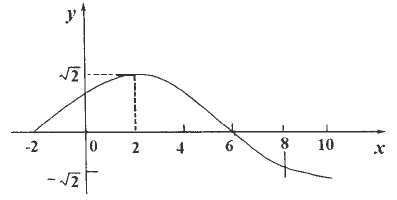
(1)求此函數的解析式f1(x)；

(2)與f1(x)的圖象關于x＝8對稱的函數解析式f2(x)；求f1(x)＋f2(x)單增區間

答案：
解析：

 　　(1)f1(x)＝ sin( X＋ )

　　(1)f1(x)＝sin(X＋)

　　(2)當2kπ－π≤≤2kπ　k∈Z時，即16k－8≤x≤16時，f1(x)＋f2(x)為增函數即單調增區間為[16k－8，16k]k∈Z．


練習冊系列答案
相關習題

科目：高中數學 來源：成功之路·突破重點線·數學（學生用書） 題型：022

已知F1，F2是橢圓＋＝1(________)的兩個焦點，P是橢圓上一點，且∠F1PF2＝，則△F1PF2的面積是b2．請將題目中空缺的一個可能條件填入“________”處．

查看答案和解析>>

科目：高中數學 來源：中學教材標準學案　數學　高二上冊 題型：044

解答題

已知橢圓的兩焦點為F1(－1，0)、F2(1，0)，P為橢圓上一點，且2|F1F2|＝|PF1|＋|PF2|．

(1)求此橢圓的方程；

(2)若∠F1PF2＝，求△PF1F2的面積．

查看答案和解析>>

科目：高中數學 來源：中學教材標準學案　數學　高二上冊 題型：044

解答題

已知F1(－3，0)、F2(3，0)分別是橢圓的左、右焦點，P是橢圓上一點，滿足PF1⊥PF2，∠F1PF2的平分線交F1F2于M(1，0)，求橢圓的方程．

查看答案和解析>>

科目：高中數學 來源：潮陽一中2007屆高三摸底考試、文科數學 題型：044

解答題

已知焦點在x軸上的雙曲線C的兩條漸近線過坐標原點，且兩條漸近線與以點為圓心，1為半徑為圓相切，又知C的一個焦點與A關于直線y＝x對稱．

(1)

求雙曲線C的方程；

(2)

若Q是雙曲線C上的任一點，F1、F2為雙曲線C的左、右兩個焦點，從F1引∠F1QF2的平分線的垂線，垂足為N，試求點N的軌跡方程．

(3)

設直線y＝mx＋1與雙曲線C的左支交于A、B兩點，另一直線L經過M(－2，0)及AB的中點，求直線L在y軸上的截距b的取值范圍．

查看答案和解析>>

同步練習冊答案