
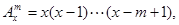 其中x∈R,m為正整數,且
其中x∈R,m為正整數,且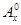 =1,這是排列數A
=1,這是排列數A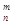 (n,m是正整數,且m≤n)的一種推廣.
(n,m是正整數,且m≤n)的一種推廣.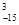 的值; (2)確定函數
的值; (2)確定函數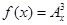 的單調區間.
的單調區間.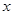 的方程
的方程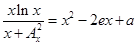 只有一個實數根, 求
只有一個實數根, 求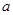 的值.
的值.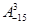 =(-15)(-16)(-17)=4080;
=(-15)(-16)(-17)=4080; 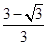 ),(
),(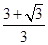 ,+∞);減區間為[
,+∞);減區間為[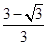 ,
,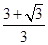 ];
];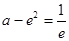 , 即
, 即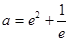 時, 方程
時, 方程 只有一個根.
只有一個根. 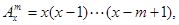 可求出
可求出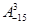 =(-15)(-16)(-17)=4080.
=(-15)(-16)(-17)=4080.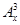 )/=3x2-6x+2.根據導數大于零,求單調增區間.導數小于零,求單調減區間.
)/=3x2-6x+2.根據導數大于零,求單調增區間.導數小于零,求單調減區間.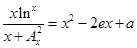 , 得
, 得
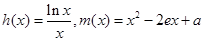 ,然后利用導數確定h(x)的圖像,作出m(x)的圖像,根據圖像可確定它們有一個公共點時,a的取值范圍.
,然后利用導數確定h(x)的圖像,作出m(x)的圖像,根據圖像可確定它們有一個公共點時,a的取值范圍.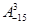 =(-15)(-16)(-17)=4080;………3分
=(-15)(-16)(-17)=4080;………3分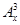 )/=3x2-6x+2.令3x2-6x+2>0,解得x<
)/=3x2-6x+2.令3x2-6x+2>0,解得x<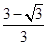 或x>
或x>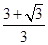
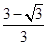 )時,函數為增函數,當x∈(
)時,函數為增函數,當x∈(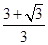 ,+∞)時,函數也為增函數.
,+∞)時,函數也為增函數.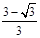 ≤x≤
≤x≤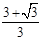 ,因此,當x∈[
,因此,當x∈[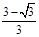 ,
,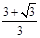 ]時,函數為減函數.
]時,函數為減函數. 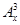 的增區間為(-∞,
的增區間為(-∞,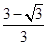 ),(
),(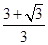 ,+∞);減區間為[
,+∞);減區間為[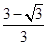 ,
,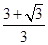 ]……7分
]……7分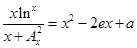 , 得
, 得 .
. , 則
, 則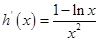 .………8分
.………8分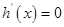 , 得
, 得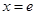 .
.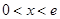 時,
時, 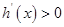 ; 當
; 當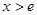 時,
時, 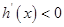 .
.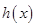 在區間
在區間 上單調遞增, 在區間
上單調遞增, 在區間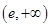 上單調遞減.
上單調遞減.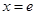 時, 函數
時, 函數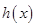 取得最大值, 其值為
取得最大值, 其值為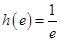 . …… 10分
. …… 10分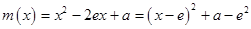 ,
,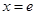 時, 函數
時, 函數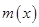 取得最小值, 其值為
取得最小值, 其值為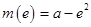 . …… 12分
. …… 12分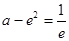 , 即
, 即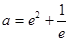 時, 方程
時, 方程 只有一個根. …… 14分
只有一個根. …… 14分

科目:高中數學 來源:不詳 題型:解答題
 ,對給定的正整數
,對給定的正整數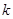 ,若在其定義域內存在實數
,若在其定義域內存在實數 ,使得
,使得 ,則稱函數
,則稱函數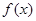 為“
為“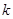 性質函數”。
性質函數”。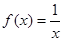 是否為“
是否為“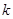 性質函數”?說明理由;
性質函數”?說明理由;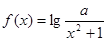 為“2性質函數”,求實數
為“2性質函數”,求實數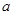 的取值范圍;
的取值范圍;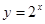 與
與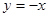 的圖像有公共點,求證:
的圖像有公共點,求證: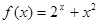 為“1性質函數”。
為“1性質函數”。查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
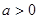 ,函數
,函數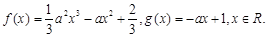
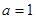 時,求函數
時,求函數 在點(1,
在點(1,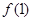 )的切線方程;
)的切線方程; 在[-1,1]的極值;
在[-1,1]的極值;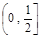 上至少存在一個實數x0,使
上至少存在一個實數x0,使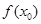 >g(xo)成立,求正實數
>g(xo)成立,求正實數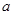 的取值范圍。
的取值范圍。查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
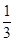 x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函數,則m的取值范圍是( )
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函數,則m的取值范圍是( )| A.m<2或m>4 | B.-4<m<-2 | C.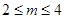 | D.以上皆不正確 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com