中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

已知圓內接四邊形ABCD的邊長分別為AB=2，BC=6，CD=DA=4，求四邊形ABCD的面積.

S=16sin120°=8


解析:

如圖: 連結BD，則有四邊形ABCD的面積: 

S=S△ABD+S△CDB=·AB·ADsinA+·BC·CD·sinC

∵A+C=180°，∴sinA=sinC

故S=(AB·AD+BC·CD)sinA=(2×4+6×4)sinA=16sinA

由余弦定理，在△ABD中，BD2=AB2+AD2－2AB·AD·cosA=20－16cosA

在△CDB中，BD2=CB2+CD2－2CB·CD·cosC=52－48cosC

∴20－16cosA=52－48cosC，∵cosC=－cosA，

∴64cosA=－32，cosA=－，

又0°＜A＜180°，∴A=120°故S=16sin120°=8.

練習冊系列答案
相關習題

科目：高中數(shù)學 來源： 題型：

已知圓內接四邊形ABCD的邊長分別為AB=2，BC=6，CD=DA=4求四邊形ABCD的面積．

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：

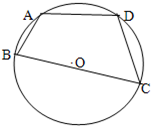精英家教網(wǎng)如圖，已知圓內接四邊形ABCD的邊長分別為AB=2，BC=6，AD=CD=4．
（1）求角A的度數(shù)；
（2）求四邊形ABCD的面積．

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：

如圖，已知圓內接四邊形ABCD的邊長為AB=2，BC=6，CD=DA=4，則四邊形ABCD面積為（　　）

查看答案和解析>>

科目：高中數(shù)學 來源： 題型：

如圖已知圓內接四邊形ABCD中，AB=2，BC=6，AD=CD=4，則四邊形ABCD的面積S=
8
3
8
3
．

查看答案和解析>>

科目：高中數(shù)學 來源：江蘇省私立無錫光華學校2009—2010學年高二第二學期期末考試 題型：解答題

本題滿分16分）已知圓內接四邊形ABCD的邊長分別為AB = 2，BC = 6，CD = DA = 4；求四邊形ABCD的面積．

查看答案和解析>>

同步練習冊答案