
已知函數 .
.
(1)請用“五點法”畫出函數 在長度為一個周期的閉區間上的簡圖(先在所給的表格中填上所需的數值,再畫圖);
在長度為一個周期的閉區間上的簡圖(先在所給的表格中填上所需的數值,再畫圖);
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(2)求函數 的單調遞增區間;
的單調遞增區間;
(3)當 時,求函數
時,求函數 的最大值和最小值及相應的
的最大值和最小值及相應的 的值.
的值.
(1)過程見解析;(2)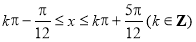 ;(3)當x=0時,函數取得最小值
;(3)當x=0時,函數取得最小值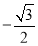 ;當x=
;當x=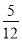 ?時,函數取得最大值1.
?時,函數取得最大值1.
【解析】
試題分析:(1)畫三角函數圖象的方法是五點法,具體步驟是1.列表,標出一個周期內與x軸的交點和最大值點與最小值點;2.描點,將列出的5個點畫在平面直角坐標系中;3.連線,用平滑的曲線連接5點;由題,列表如下,描點連線; (2)三角函數sinx在[-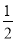 ?,
?,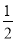 ?]上遞增,在[
?]上遞增,在[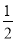 ?,
?,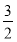 ?]上遞減,由題,令
?]上遞減,由題,令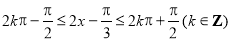 ,可解得
,可解得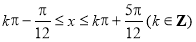 ,故函數f(x)在
,故函數f(x)在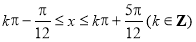 遞增;(3)由x的范圍可以得到2x-
遞增;(3)由x的范圍可以得到2x-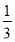 ?的范圍,再由(2)中函數的增減性可以求得最大值和最小值.
?的范圍,再由(2)中函數的增減性可以求得最大值和最小值.
試題解析:(1)令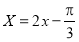 ,則
,則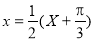 .填表:
.填表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
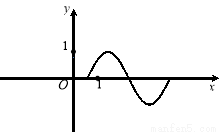
(2)令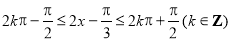 ,
,
解得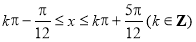 ,
,
∴函數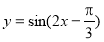 的單調增區間為
的單調增區間為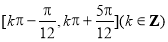 .
.
(3)∵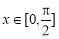 ,
,
∴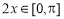 ,
,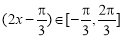
∴當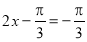 ,即
,即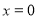 時,
時,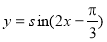 取得最小值
取得最小值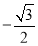 ;
;
當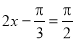 ,即
,即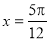 時,
時,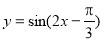 取得最大值1.
取得最大值1.
考點:1.五點法作函數y=Asin(ωx+φ)的圖象;2.三角函數的單調區間;3.三角函數的最值.


 53天天練系列答案
53天天練系列答案科目:高中數學 來源:2016屆吉林白山市高一上學期期末考試數學卷(解析版) 題型:選擇題
側棱長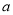 為的正三棱錐
為的正三棱錐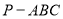 的側面都是直角三角形,且四個頂點都在一個球面上,則球的表面積為( )
的側面都是直角三角形,且四個頂點都在一個球面上,則球的表面積為( )
A. 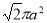 B.
B.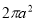 C.
C. D.
D.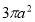
查看答案和解析>>
科目:高中數學 來源:2015屆重慶市高二上學期期末考試文科數學試卷(解析版) 題型:選擇題
從三男三女6名學生中任選2名(每名同學被選中的機會相等),則2名都是女同學的概率等于( )
A.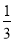 B.
B.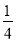 C.
C.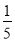 D.
D.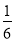
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com