Question

如圖所示，正方形ABCD與正方形ABEF所在平面互相垂直，兩個(gè)正方形邊長(zhǎng)均為2，M、N分別是AC和BF上的點(diǎn)，且AM=FN=x．

（1）求證：MN∥平面BCE;

（2）設(shè)MN=y,求函數(shù)y=f(x);

（3）當(dāng)MN最短時(shí),求MN與AC、MN與FB所成的角.

Answer 1

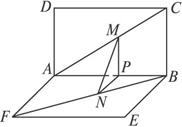
思路解析：本題已知了面面垂直關(guān)系,容易想到利用面面垂直的性質(zhì),從而構(gòu)造得到線面垂直關(guān)系.第一問(wèn)要證明線面平行,緊緊圍繞著線面平行的判定定理,去尋求相關(guān)的線線平行,充分利用正方形的性質(zhì),從而得到線線平行;第二問(wèn),在第一問(wèn)的基礎(chǔ)上,在相關(guān)的三角形中將MN表示出來(lái),進(jìn)而將第三個(gè)問(wèn)題解決.

解：（1）作MP⊥AB于P，則有MP⊥平面ABFE.

連結(jié)PN，又BC⊥平面ABCD，

∴MP∥BC.∴.

又AM=FN,AC=FB,

∴.∴PN∥AF∥BE.

故平面MPN∥平面BCE.MN平面MPN,∴MN∥平面BCE．

（2）∵AM=x，MP=AP=x，

又PN=PB=，

從而由MP⊥平面ABFE知MP⊥PN,MN=.

∴y=（0

（3）由（2）得y=.當(dāng)x=1時(shí),MN有最小值為1,此時(shí)M、N分別為兩個(gè)正方形的中心,∴.

∴MN∥EC.

∴MN與AC所成的角是∠ACE（或其補(bǔ)角）.

易知△ACE為正三角形,故MN與AC所成的角是60°.

同理，MN與FB所成的角是60°.