
對于無窮數(shù)列 和函數(shù)
和函數(shù)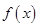 ,若
,若 ,則稱
,則稱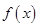 是數(shù)列
是數(shù)列 的母函數(shù).
的母函數(shù).
(Ⅰ)定義在 上的函數(shù)
上的函數(shù) 滿足:對任意
滿足:對任意 ,都有
,都有 ,且
,且 ;又數(shù)列
;又數(shù)列 滿足:
滿足: .
.
求證:(1) 是數(shù)列
是數(shù)列 的母函數(shù);
的母函數(shù);
(2)求數(shù)列 的前項
的前項 和
和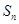 .
.
(Ⅱ)已知 是數(shù)列
是數(shù)列 的母函數(shù),且
的母函數(shù),且 .若數(shù)列
.若數(shù)列 的前
的前 項和為
項和為 ,求證:
,求證: .
.
(Ⅰ)(1) 由題知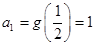 ,
,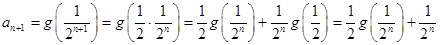
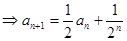
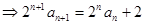 ,
,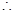
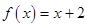 是數(shù)列
是數(shù)列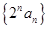 的母函數(shù)
的母函數(shù)
(2) 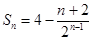 (Ⅱ)
(Ⅱ)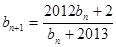 ,
,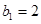 ,
,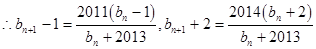
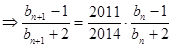 從而
從而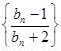 是以
是以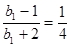 為首項,
為首項,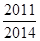 為公比的等比數(shù)列
為公比的等比數(shù)列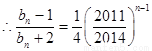
又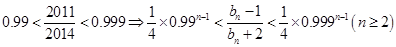 故當
故當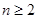 時,有
時,有
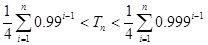
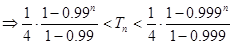 ,化簡得結論
,化簡得結論
【解析】
試題分析:(Ⅰ)(1)由題知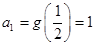 ,且
,且
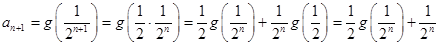
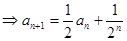
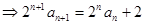 .
.
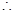
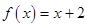 是數(shù)列
是數(shù)列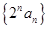 的母函數(shù);
的母函數(shù);
(2) 由(1) 知: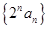 是首項和公差均為
是首項和公差均為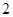 的等差數(shù)列,故
的等差數(shù)列,故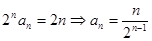 .
.
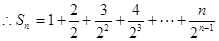 ①
①
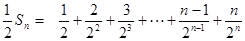 ②
②
①-②得: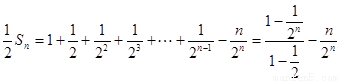
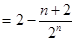 .
.
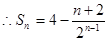 .
.
(Ⅱ)由題知: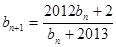 ,
,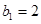 .
. 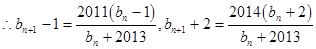
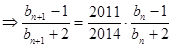 .
.
從而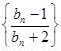 是以
是以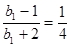 為首項,
為首項,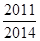 為公比的等比數(shù)列.
為公比的等比數(shù)列.
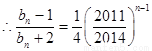 .
.
又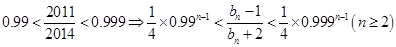
故當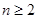 時,有:
時,有:
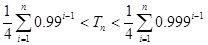
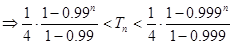
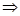
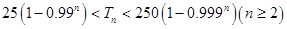 .
.
考點:信息題及數(shù)列求和
點評:求解本題首先要正確理解所給信息母函數(shù)的實質,將其性質代入相應的函數(shù)式中推理;第一問的數(shù)列求和用到了錯位相減法,這種方法是數(shù)列求和題常用到的方法,其適用于通項公式為關于n的一次函數(shù)式與指數(shù)式的乘積形式的數(shù)列


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優(yōu)測試卷系列答案
黃岡海淀全程培優(yōu)測試卷系列答案科目:高中數(shù)學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2n |
| 2012x+2 |
| x+2013 |
| bn-1 |
| bn+2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
對于無窮數(shù)列![]() 和函數(shù)
和函數(shù)![]() ,若
,若![]() ,則稱
,則稱![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù).
的母函數(shù).
(Ⅰ)定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足:對任意
滿足:對任意![]() ,都有
,都有![]() ,且
,且![]() ;又數(shù)列
;又數(shù)列![]() 滿足:
滿足:![]() .
.
(1) 求證:![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù);
的母函數(shù);
(2)求數(shù)列![]() 的前項
的前項![]() 和
和![]() .
.
(Ⅱ)已知![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù),且
的母函數(shù),且![]() .若數(shù)列
.若數(shù)列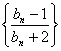 的前
的前![]() 項和為
項和為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
對于無窮數(shù)列![]() 和函數(shù)
和函數(shù)![]() ,若
,若![]() ,則稱
,則稱![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù).
的母函數(shù).
(Ⅰ)定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足:對任意
滿足:對任意![]() ,都有
,都有![]() ,且
,且![]() ;又數(shù)列
;又數(shù)列![]() 滿足:
滿足:![]() .
.
(1) 求證:![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù);
的母函數(shù);
(2)求數(shù)列![]() 的前項
的前項![]() 和
和![]() .
.
(Ⅱ)已知![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù),且
的母函數(shù),且![]() .若數(shù)列
.若數(shù)列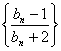 的前
的前![]() 項和為
項和為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
對于無窮數(shù)列![]() 和函數(shù)
和函數(shù)![]() ,若
,若![]() ,則稱
,則稱![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù).
的母函數(shù).
(Ⅰ)定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足:對任意
滿足:對任意![]() ,都有
,都有![]() ,且
,且![]() ;又數(shù)列
;又數(shù)列![]() 滿足:
滿足:![]() .
.
(1) 求證:![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù);
的母函數(shù);
(2)求數(shù)列![]() 的前項
的前項![]() 和
和![]() .
.
(Ⅱ)已知![]() 是數(shù)列
是數(shù)列![]() 的母函數(shù),且
的母函數(shù),且![]() .若數(shù)列
.若數(shù)列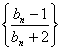 的前
的前![]() 項和為
項和為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com